Resistance of a Conductor
While wire of any size or resistance value may be
used, the word “conductor" usually refers to materials
that offer low resistance to current flow, and the
word “insulator" describes materials that offer high resistance to current. There is no distinct dividing line
between conductors and insulators; under the proper
conditions, all types of material conduct some current.
Materials offering a resistance to current flow
midway between the best conductors and the poorest
conductors (insulators) are sometimes referred to as
“semiconductors," and find their greatest application
in the field of transistors.
The best conductors are materials, chiefly metals,
which possess a large number of free electrons;
conversely, insulators are materials having few free
electrons. The best conductors are silver, copper, gold,
and aluminum; but some nonmetals, such as carbon
and water, can be used as conductors. Materials such
as rubber, glass, ceramics, and plastics are such poor
conductors that they are usually used as insulators. The
current flow in some of these materials is so low that
it is usually considered zero. The unit used to measure
resistance is called the ohm. The symbol for the ohm is
the Greek letter omega (O). In mathematical formulas,
the capital letter “R" refers to resistance. The resistance
of a conductor and the voltage applied to it determine
the number of amperes of current flowing through the
conductor. Thus, 1 ohm of resistance will limit the
current flow to 1 ampere in a conductor to which a
voltage of 1 volt is applied.
Factors Affecting Resistance
- The resistance of a metallic conductor is dependent
on the type of conductor material. It has been
pointed out that certain metals are commonly used
as conductors because of the large number of free
electrons in their outer orbits. Copper is usually
considered the best available conductor material,
since a copper wire of a particular diameter offers a
lower resistance to current flow than an aluminum
wire of the same diameter. However, aluminum is
much lighter than copper, and for this reason as well
as cost considerations, aluminum is often used when
the weight factor is important.
- The resistance of a metallic conductor is directly
proportional to its length. The longer the length of a
given size of wire, the greater the resistance. Figure
10-40 shows two wire conductors of different
lengths. If 1 volt of electrical pressure is applied
across the two ends of the conductor that is 1 foot
in length and the resistance to the movement of free
electrons is assumed to be 1 ohm, the current flow
is limited to 1 ampere. If the same size conductor is
doubled in length, the same electrons set in motion
by the 1 volt applied now find twice the resistance;consequently, the current flow will be reduced by
one-half.
- The resistance of a metallic conductor is inversely
proportional to the cross-sectional area. This area
may be triangular or even square, but is usually
circular. If the cross-sectional area of a conductor
is doubled, the resistance to current flow will
be reduced in half. This is true because of the
increased area in which an electron can move
without collision or capture by an atom. Thus, the
resistance varies inversely with the cross-sectional
area of a conductor.
- The fourth major factor influencing the resistance
of a conductor is temperature. Although some
substances, such as carbon, show a decrease
in resistance as the ambient (surrounding)
temperature increases, most materials used as
conductors increase in resistance as temperature
increases. The resistance of a few alloys, such as
constantan and Manganin™, change very little as
the temperature changes. The amount of increase in
the resistance of a 1 ohm sample of a conductor, per
degree rise in temperature above 0° Centigrade (C),
the assumed standard, is called the temperature
coefficient of resistance. For each metal, this is a
different value; for example, for copper the value
is approximately 0.00427 ohm. Thus, a copper wire
having a resistance of 50 ohms at a temperature
of 0 °C will have an increase in resistance of 50
× 0.00427, or 0.214 ohm, for each degree rise
in temperature above 0 °C. The temperature
coefficient of resistance must be considered where
there is an appreciable change in temperature of a conductor during operation. Charts listing the
temperature coefficient of resistance for different
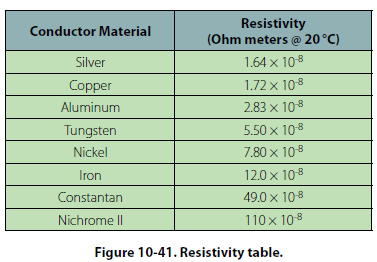
materials are available. Figure 10-41 shows a table for
“resistivity" of some common electric conductors.
The resistance of a material is determined by four
properties: material, length, area, and temperature.
The first three properties are related by the following
equation at T = 20 °C (room temperature):

|

