Our customary system of measurement (figure 1-23) is part of our cultural heritage from the days when the thirteen colonies were under British rule. It started as a hodge-podge of Anglo-Saxon, Roman, and Norman-French weights and measures. Since medieval times, commissions appointed by various English monarchs had reduced the chaos of measurement by setting specific standards for some of the most important units. Early records, for instance, indicate that an inch was defined as the length of "three barleycorns, round and dry" when laid together; a pennyweight, or one-twentieth of a Tower ounce, was equal to 32 wheatcorns from the "midst of the ear." The U.S. gallon is the British wine gallon, standardized at the beginning of the 18th century (and about 20 percent smaller than the Imperial gallon that the British adopted in 1824 and have since used to measure most liquids). In short, as some of the founders of this country realized, the customary system was a makeshift based largely on folkways. Metric System
The metric system is the dominant language of measurement in use today. Most of the world countries used the metric system prior to World War II. Since the war, more countries have converted or are in the process of converting to the metric system. Only the United States and 13 smaller countries have not made the conversion. Congress has the power to define the standard of weights and measures. Repeatedly the metric system has been proposed and each time the question has been voted down.
	Figure 1-23 Some common units

The metric system was developed by a French statesman, Talleyrand, Bishop of Autum, using a "meter" as a standard; the meter being a specific portion of the circumference of the earth at the equator. From this base measurement the meter was developed and accepted as the standard. Divisions and multiples of the meter are based on the decimal system.

The Logic of Metric

No other system of measurement that has been actually used can match the inherent simplicity of International Metric. It was designed deliberately to fill all the needs of scientists and engineers. Laymen need only know and use a few simple parts of it. It is logically streamlined, whereas other systems developed more or less haphazardly. At this time there are only six base units in the International Metric System. The unit of length is the meter. The unit of mass is the kilogram. The unit of time is the second. The unit of electric current is the ampere. The unit of temperature is the kelvin (which in common use is translated into the degree Celsius, formerly called degree centigrade). The unit of luminous intensity is the candela.

All the other units of measurement in the International Metric System are derived from these six base units. Area is measured in square meters; speed in meters per second; density in kilograms per cubic meter. The newton, the unit of force, is a simple relationship involving meters, kilograms, and seconds; and the pascal, unit of pressure, is defined as one newton per square meter. In some other cases, the relationship between the derived and base units must be expressed by rather more complicated formulas - which is inevitable in any measurement system, owing to the innate complexity of some of the things we measure. Similar relationships among mass, area, time and other quantities in the customary system usually require similar formulas, made all the more complicated because they can contain arbitrary constants. For example, one horsepower is defined as 550 foot-pounds per second.

The third intrinsic advantage is that metric is based on the decimal system. Multiples and submultiples of any given unit are always related by powers of 10. For instance, there are 10 millimeters in one centimeter; 100 centimeters in one meter; and 1,000 meters in one kilometer. This greatly simplifies converting larger to smaller measurements. For example, in order to calculate the number of meters in 3.794 kilometers, multiply by 1,000 (move the decimal point three places to the right) and the answer is 3,794. For comparison, in order to find the number of inches in 3.794 miles, it is necessary to multiply first by 5,280 and then by 12.
 

Moreover, multiples and submultiples of all the International Metric units follow a consistent naming scheme, which consists of attaching a prefix to the unit, whatever it may be. For example, kilo stands for 1,000: one kilometer equals 1,000 meters, and one kilogram equals 1,000 grams. Micro is the prefix for one millionth: one meter equals one million micrometers, and one gram equals one million micrograms (figure 1-24). 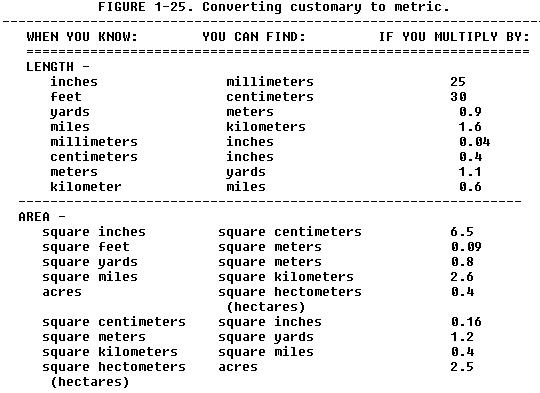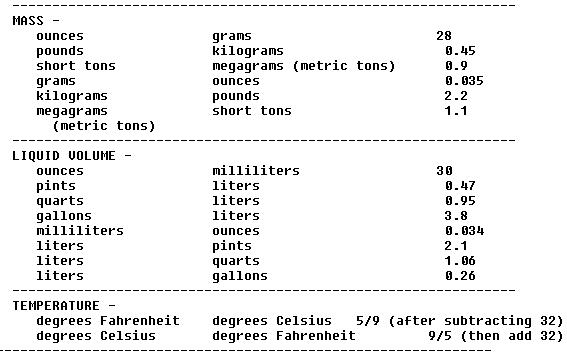Conversion: Metric To Conventional

People tend to resist changes, usually because they do not understand either the purpose of the change or the new order. Terminology for customary units and metric units have been discussed. A conversion table also has been included. Examples of its use follow:

To convert inches to millimeters, multiply the number of inches by 25. (Ex. 25 into mm = 25 x 25 = 625 mm)
To convert millimeters to inches multiply millimeters by 0.04. (Ex. 625 mm x 0.04 = 25 inches.)
To convert square inches to square centimeters multiply by 6.5. (Ex. 100 sq in x 6.5 = 650 sq cm)
To convert square centimeters to square inches multiply by 0.16. (Ex. 100 x 0.16 = 16 sq in)
 

Figure 1-26

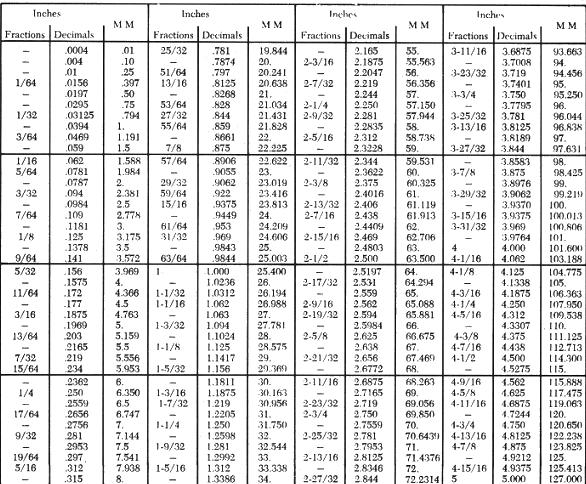
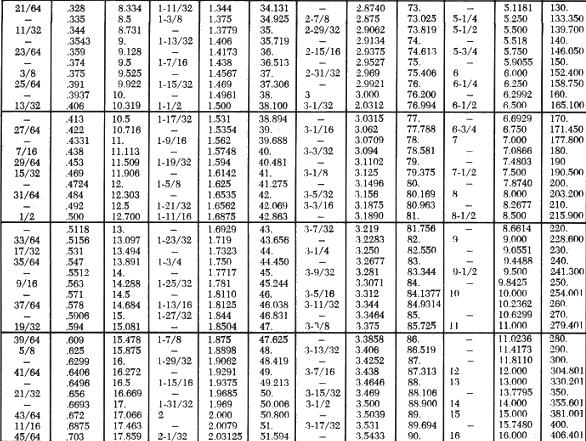
Figure 1-26 is practically self explanatory. Measurements starting at 1/64 inch up to 20 inches have been converted to decimal divisions of inches and to millimeters.