Work

The study of machines, both simple and complex, is in one sense a study of the energy of mechanical work. This is true because all machines transfer input energy, or the work done on the machine to output energy, or the work done by the machine.

Work, in the mechanical sense of the term, is done when a resistance is overcome by a force acting through a measurable distance. Two factors are involved: (1) Force and (2) movement through a distance. As an example, suppose a small aircraft is stuck in the snow. Two men push against it for a period of time, but the aircraft does not move. According to the technical definition, no work was done in pushing against the aircraft. By definition, work is accomplished only when an object is displaced some distance against a resistive force.

In equation form, this relationship is,

Work = Force (F) x distance (d).

The physicist defines work as "work is force times displacement. Work done by a force acting as a body is equal to the magnitude of the force multiplied by the distance through which the force acts."

In the metric system, the unit of work is the joule, where one joule is the amount of work done by a force of one newton when it acts through a distance of one meter. That is,    1 joule = 1 newton-m

Hence we can write the definition in the form  W (joules) = F (newtons) x d (meters). If we push a box for 8 m across a floor with a force of 100 newtons, the work we perform is   W = Fd = 100 newtons x 8m = 800 joules

How much work is done in raising a 500 kg (kilogram) elevator cab from the ground floor of a building to its tenth floor, 30 m (meters) higher? We note that the force needed is equal to the weight of the cab, which is mg.

In the metric system, mass rather than weight is normally specified. To find the weight in newtons (the metric unit of force) of something whose mass in kilograms is known, we simply turn to F = mg and set G = 9.8 m/SEC2

F (newtons) = M (kilograms) x G (9.8 m/sec2)
W (joules) = M (kilograms) x G (9.8 m/sec2) x D (meters)
W = Fd = mgd = 500 kg x 9.8 m/Sec2 x 30m
= 147,000 joules
= 1.47 x 105 joules

Force Parallel To Displacement

If force is expressed in pounds and distances in feet, work will be expressed in ft-lbs (foot-pounds). Example: How much work is accomplished in lifting a 40 pound weight to a vertical height of 25 feet?

W = Fd
= 40 x 25
= 1,000 ft-lb.

Example: How much work is accomplished in pushing a small aircraft into a hangar a distance of 115 feet if a force of 75 pounds is required to keep it moving?

W = Fd
= 75 x 115
= 8,625 ft-lb.

Force Not Parallel To Displacement

In this equation, F is assumed to be in the same direction as d. If it is not, for example the case of a body pulling a wagon with a rope not parallel to the ground, we must use F for the component of the applied force that acts in the direction of the motion, figure 7-37(A).

The component of a force in the direction of a displacement d is:   F cos .  Where  is the angle between F and d. Hence the most general equation for work is  W = Fd cos .

When F and d are parallel,  = 0 and cos  = 1, so that Fd cos  reduces to just Fd. When F and d are perpendicular,  = 90° and cos  = 0, so that no work is done. A force that is perpendicular to the motion of an object can do no work upon it. Thus gravity, which results in a downward force on everything near the earth, does no work on objects moving horizontally along the earth's surface. However, if we drop an object, as it falls to the ground work is definitely done upon it.

{See unreferenced figure 7-36. Direction of work.}

Friction

In calculating work done, the actual resistance overcome is measured. This is not necessarily the weight of the object being moved. This point can be illustrated by referring to figure 7-37. A 900 pound load is being pulled a distance of 200 feet. This does not mean that the work done (force x distance) is 180,000 foot-pounds (900 pounds x 200 feet). This is because the man pulling the load is not working against the total weight of the load, but rather against the rolling friction of the cart, which may be no more than 90 pounds.

Friction is one of the most important aspects of life. Without friction it would be impossible to walk. One would have to shove oneself from place to place, and would have to bump against some obstacle to stop at a destination. Yet friction is a liability as well as an asset, and requires consideration when dealing with any moving mechanism.

In experiments relating to friction, measurement of the applied forces reveals that there are three kinds of friction. One force is required to start a body moving, while another is required to keep the body moving at constant speed. Also, after a body is once in motion, a definitely larger force is required to keep it sliding than to keep it rolling.

Thus, the three kinds of friction may be classified as: (1) Starting (static) friction, (2) sliding friction, and (3) rolling friction.

Static Friction

When an attempt is made to slide a heavy object along a surface, the object must first be broken loose or started. Once in motion, it slides more easily. The "breaking loose" force is, of course, proportional to the weight of the body. The force necessary to start the body moving slowly is designated "F," and "F'" is the normal force pressing the body against the surface (usually its weight). Since the nature of the surfaces rubbing against each other is important, they must be considered. The nature of the surfaces is indicated by the coefficient of starting friction which is designated by the letter "k." This coefficient can be established for various materials and is often published in tabular form. Thus, when the load (weight of the object) is known, starting friction can be calculated by using the equation,

F = kF'

For example, if the coefficient of sliding friction of a smooth iron block on a smooth, horizontal surface is 0.3, the force required to start a 10 pound block would be 3 pounds; a 40 pound block, 12 pounds.

Starting friction for objects equipped with wheels and roller bearings is much smaller than that for sliding objects. Nevertheless, a locomotive would have difficulty getting a long train of cars in motion all at one time. Therefore, the couples between the cars are purposely made to have a few inches of play. When the engineer is about to start the train, he backs the engine until all the cars are pushed together. Then, with a quick start forward the first car is set in motion. This technique is employed to overcome the static friction of each wheel (as well as the inertia of each car). It would be impossible for the engine to start all of the cars at the same instant, for static friction, which is the resistance of being set in motion, would be greater than the force exerted by the engine. Once the cars are in motion, however, static friction is greatly reduced and a smaller force is required to keep the train in motion than was required to start it.

Sliding Friction

Sliding friction is the resistance to motion offered by an object sliding over a surface. It pertains to friction produced after the object has once been set into motion, and is always less than starting friction. The amount of sliding resistance is dependent on the nature of the surface of the object, the surface over which it slides, and the normal force between the object and the surface. This resistive force may be computed by the formula,

F = N

where: "F" is the resistive force due to friction expressed in pounds; "N" is the force exerted on or by the object perpendicular (normal) to the surface over which it slides; and "" (mu) is the coefficient of sliding friction. (On a horizontal surface, N is equal to the weight of the object in pounds.) The area of the sliding object exposed to the sliding surface has no effect on the results. A block of wood, for example, will not slide any easier on one of the broad sides than it will on a narrow side, (assuming all sides have the same smoothness). Therefore, area does not enter into the equation above.

Rolling Friction

Resistance to motion is greatly reduced if an object is mounted on wheels or rollers. The force of friction for objects mounted on wheels or rollers is called rolling friction. This force may be computed by the same equation used in computing sliding friction, but the values of mu will be much smaller. For example, mu for rubber tires on concrete or macadam is about 0.02. The value of  for roller bearings is very small, usually ranging from 0.001 to 0.003 and is often disregarded.

Example: An aircraft with a gross weight of 79,600 lbs is towed over a concrete ramp. What force must be exerted by the towing vehicle to keep the airplane rolling after once set in motion?

F = N
   = 0.02 X 79,600 = 1,592 lb.

Power

Power is a badly abused term. In speaking of power driven equipment, people often confuse the term "power" with the ability to move heavy loads. This is not the meaning of power. A sewing machine motor is powerful enough to rotate an aircraft engine propeller providing it is connected to the crankshaft through a suitable mechanism. It could not rotate the propeller at 2,000 rpm, however, for it is not powerful enough to move a large load at a high speed. Power, thus, means rate of doing work. It is measured in terms of work accomplished per unit of time. In equation form, it reads:

If force is expressed in pounds, distance in feet, and time in seconds, then power is given in ft-lbs/sec (foot-pounds per second). Time may also be given in minutes. If time in minutes is used in this equation, then power will be expressed in ft-lbs/min.

Example:

An aircraft engine weighing 3,500 pounds was hoisted a vertical height of 7 feet in order to install it on an aircraft. The hoist was hand powered and required 3 minutes of cranking to raise the engine. How much power was developed by the man cranking the hoist? (Neglect friction in the hoist.)

Power is often expressed in units of horsepower. One horsepower is equal to 550 ft-lbs/sec or 33,000 ft-lbs/min.

Example:

In the hoist example above, calculate the horsepower developed by the man.

Power in ft-lbs/min

Power is rate of doing work:

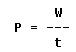
In the metric system the unit of power is the watt, where  1 watt = 1 joule/sec

The watt is the metric unit of power, thus a motor with a power output of 5,000 watts is capable of doing 5,000 joules of work per second.

A kilowatt (kw) is equal to 1,000 watts. Hence the above motor has a power output of 5 kw.

How much time does the elevator cab of the previous example need to ascend 30 meters if it is being lifted by a 5 kw motor? We rewrite P = W/t in the form

and then substitute w = 1.47 x 105 joules and p = 5.103 watts to find that

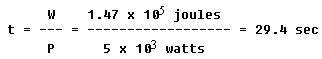
Energy

In many cases when work is done on an object, something is given to the object which it retains and which later enables it to do work. When a weight is lifted to a certain height such as in the case of a trip hammer, or when a clock spring is wound, the object acquires, through having work done on it, the ability to do work itself. In storage batteries and gasoline, energy is stored which can be used later to do work. Energy stored in coal or food can be used to do work. This storage gives such objects the ability to do work; thus, energy is defined as the ability to do work.

In general, a change in energy is equal to the work done; the loss in energy of a body may be measured by the work it does, or the gain in energy of a body may be measured by the amount of work done on it. For convenience, energy which bodies possess is classified into two categories: (1) Potential and (2) kinetic.

Potential energy may be classified into three groups: (1) That due to position, (2) that due to distortion of an elastic body, and (3) that which produces work through chemical action. Water in an elevated reservoir, and the lifted weight of a pile driver are examples of the first group; a stretched rubber band or compressed spring are examples of the second group; and energy in coal, food, and storage batteries are examples of the third group.

Bodies in motion required work to put them in motion. Thus, they possess energy of motion. Energy due to motion is known as kinetic energy. A moving vehicle, a rotating flywheel, and a hammer in motion are examples of kinetic energy.

Energy is expressed in the same units as those used to express work. The quantity of potential energy possessed by an elevated weight may be computed by the equation,

Potential Energy = Weight x Height.

If weight is given in pounds and height in feet, the final unit of energy will be ft-lbs (foot-pounds).

Example: An aircraft with a gross weight of 110,000 pounds is flying at an altitude of 15,000 feet above the surface of the earth. How much potential energy does the airplane possess with respect to the earth?

Potential Energy = Weight x Height
                    PE = 110,000 x 15,000
                          = 1,650,000,000 ft-lbs
 

Forms of Energy

The most common forms of energy are heat, mechanical, electrical, and chemical. The various forms of energy can be changed, or transformed, into another form in many different ways. For example, in the case of mechanical energy, the energy of work done against friction is always converted into heat energy, and the mechanical energy that turns an electric generator develops electrical energy at the output of the generator.