1-22
Forces Acting on the Airplane when at Airspeeds Slower than Cruise
| At a constant cruise speed, maintaining straight-and-level
flight, the force of thrust and drag act opposite to each other and parallel
to the flightpath. These opposing forces are equal in magnitude. Also,
the force of lift is equal in magnitude to the force of weight.
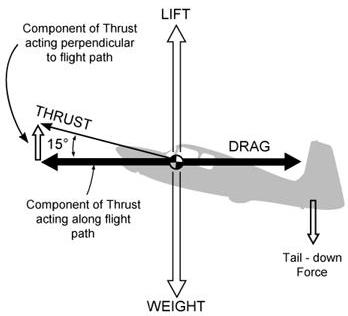
While maintaining straight-and-level flight at constant airspeeds slower
than cruise, the opposing forces must still be equal in magnitude, but
some of these forces are separated into components. In this flight condition,
the actual thrust no longer acts parallel and opposite to the flightpath
and drag. Actual thrust is inclined upward as illustrated in figure 1-36. |
|
Figure 1-36.—The forces on the airplane in straight-and-level
flight at airspeeds slower than cruise.
 |
Note that now thrust has two components; one acting perpendicular to
the flightpath in the direction of lift, while the other acts along the
flightpath. Because the actual thrust is inclined, its magnitude must be
greater than drag if its component of thrust along the flightpath is to
equal drag. Also note that a component of thrust acts 90° to the flightpath,
and thus acts in the same direction as wing lift. Figure 1-37 also illustrates
that the forces acting upward (wing lift and the component of thrust) equal
the forces acting downward (weight and tail-down force). |
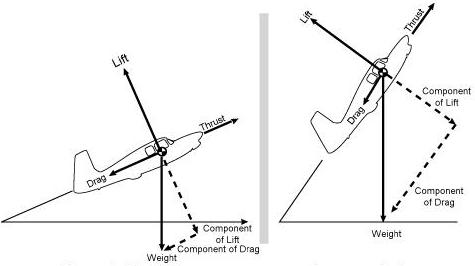
| Figure 1-37.—Forces acting on an airplane in a climb. |
|
Wing loading (wing lift) is actually less at slow speeds than at cruise
speeds because the vertical component of thrust helps support the airplane.
To summarize, in straight-and-level flight at slow speeds, the actual thrust
is greater than drag, and wing lift is less than at cruise speed.
Forces in a Climb
The forces acting on an airplane during a climb are illustrated in
figure 1-37. When the airplane is in equilibrium, the weight can be resolved
into two components: one opposing the lift, and the other acting in the
same direction as the drag along the line of the relative wind. The requirements
for equilibrium are: the thrust must equal the sum of the drag and the
opposing component of the weight; and the lift must equal its opposing
component of the weight. The steeper the angle of climb, the shorter becomes
the length of the component of lift, and simultaneously the component of
drag becomes longer. Therefore, the lift requirement decreases steadily
as the angle of climb steppens until, in a true vertical climb, if this
were possible, the wings would supply no lift and the thrust would be the
only force opposing both the drag and the weight, which would be acting
downward in opposition.
At a constant power setting, a given rate of climb can be obtained either
by climbing steeply at a low airspeed or by climbing on a shallow path
at high airspeed. At one extreme, if the airspeed is too low, the induced
drag rises to a figure at which all thrust available is required to overcome
the drag and none is available for climbing. At the other extreme, if the
speed is the maximum obtainable in level flight, again all the power is
being used to overcome the drag and there is no rate of climb. Between
these two extremes lies a speed, or a small band of speeds, which will
achieve the best rate of climb. The best rate of climb is achieved not
at the steepest angle, but at some combination of moderate angle and optimum
airspeed at which the greatest amount of excess power is available to climb
the airplane after the drag has been balanced.
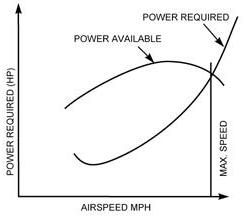
| Figure 1-38 shows that the speed for minimum drag or the
lowest point on the power-required curve, although low, is not the lowest
possible that can be flown without stalling. The increase in power required
at the lowest speeds (to the left of the minimum power-required point)
is caused by the rapidly rising effects of induced drag at the lower speeds.
The propeller driven airplane, under the same set of circumstances and
for a given rated horsepower, suffers a gradual loss of propeller efficiency
and, therefore, a gradual loss of thrust at both ends of its speed range.
The vertical distance between the power-available and power-required
curves represents the power available for climbing at the particular speed. |
|
|
Figure 1-38.—Power available vs. power required.
|
The best climbing airspeed is that at which excess power is at a
maximum so that after expending some power in overcoming drag, the maximum
amount of power remains available for climbing the airplane. At the intersection
of the curves, all the available power is being used to overcome drag,
leaving none available for climbing. Of course at the lower range, excess
power for climb soon becomes available if the angle of attack is reduced
to allow an increase in speed. [Figure 1-38]
The thrust horsepower of piston engines decreases with altitude. Even
if it is possible to prolong sea-level power to some greater altitude by
supercharging, or some other method of power boosting, the power will inevitably
decline when the boosting method employed reaches an altitude at which
it can no longer maintain a set power. At higher altitudes, the power-available
curves are lowered. Since power required increases with true airspeed (velocity),
the thrust horsepower required to fly at any desired indicated airspeed
increases with altitude.
In summarizing, it is a fallacy to think that an airplane climbs because
of “excess lift.” It does not; the airplane climbs because of power available
over power required.