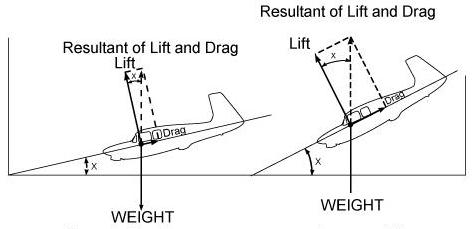
The forces acting on an airplane in a glide are illustrated in figure 1-39. For a steady glide with the engine providing no thrust, the lift, drag, and weight forces must be in equilibrium. The illustration shows that weight is balanced by the resultant of lift and drag. The lift vector, acting as it does at right angles to the path of flight, will now be tilted forward, while the drag vector will be tilted upward and will continue to act opposite to the path of flight. From the illustration, it can be seen that the geometry of the vectors is such that the angle between the lift vector and the resultant is the same as that between the glidepath and the horizontal.

Figure 1-39.—Forces acting on an airplane in a glide.

This angle (X) between the glidepath and the horizontal is called the glide angle. Further examination of this diagram will show that as drag is reduced and speed increased, the smaller will be the glide angle; therefore, the steepness of the glidepath depends on the ratio of lift to drag. When gliding at the angle of attack for best L/D, least drag is experienced, and the flattest glide will result. The L/D is a measure of the gliding efficiency or aerodynamic cleanness of the airplane. If the L/D is 11/1, it means that lift is 11 times greater than drag.

If the gliding airplane is flying at an airspeed just above the stall, it is operating at maximum angle of attack and therefore, maximum lift. This, however, does not produce the best glide angle for maximum glide distance because the induced drag at this point is high. By reducing the angle of attack, the airspeed increases and, although lift is less at the lower angle of attack, the airplane travels farther per increment of altitude lost because of greatly reduced drag. The increased range can be accomplished up to a point, by decreasing angle of attack and induced drag.

At some point, the best glide angle will be achieved. If airspeed continues to increase, the parasite drag begins to rise sharply and the airplane will again start losing more altitude per increment of distance traveled. The extreme of this is when the nose is pointed straight down.

 It can be shown that best glide distance is obtained when L/D is at maximum. This optimum condition is determined for each type of airplane and the speed at which it occurs is used as the recommended best range glide speed for the airplane. It will vary somewhat for different airplane weights, so the airspeed for a representative operational condition is generally selected.
 If several instances of the optimum glidepath were plotted by an observer on the ground under varying conditions of wind, they would be found to be inconsistent. However, the actual gliding angle of the airplane with respect to the moving air mass remains unchanged. Starting from a given altitude, a glide into the wind at optimum glide airspeed covers less distance over the ground than a glide downwind. Since in both cases the rate of descent is the same, the measured angle as seen by a ground observer is governed only by the groundspeed, being steeper at the lower groundspeed when gliding into the wind. The effect of wind, therefore, is to decrease range when gliding with a headwind component, and to increase it when gliding downwind. The endurance of the glide is unaffected by wind.

Variations in gross weight do not affect the gliding angle provided the optimum indicated airspeed for each gross weight is used. The fully loaded airplane will sink faster but at a greater forward speed, and although it would reach the ground much quicker, it would have traveled exactly the same distance as the lighter airplane, and its glide angle would have been the same.
An inspection of figure 1-39 will show that an increase in the weight factor is equivalent to adding thrust to the weight component along the glidepath.  This means more speed and, therefore, more lift and drag which lengthen the resultant vector until the geometric balance of the diagram is restored. This is done without affecting the gliding angle. The higher speed corresponding to the increased weight is provided automatically by the larger component of weight acting along the glidepath, and this component grows or diminishes in proportion to the weight. Since the gliding angle is unaffected, range also is unchanged.

Although range is not affected by changes in weight, endurance decreases with addition of weight and increases with reduction of weight. If two airplanes having the same L/D, but different weights, start a glide from the same altitude, the heavier airplane, gliding at a higher airspeed, will cover the distance between the starting point and touch down in a shorter time. Both, however, will cover the same distance. Therefore, the endurance of the heavier airplane is less.