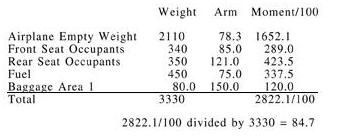
The total loaded weight of 3,330 pounds does not exceed the maximum gross weight of 3,400 pounds and the CG of 84.7 is within the 78-86 inch range; therefore, the aircraft is loaded within limits.
There are various methods for determining the loaded weight and center of gravity of an aircraft. There is the computation method, as well as methods which utilize graphs and tables provided by the aircraft manufacturer.
Computational Method
The computational method involves the application of basic math functions. The following is an example of the computational method:
Given:
Maximum Gross Weight 3400 lb
Center-of-Gravity Range 78-86 in
Front Seat Occupants 340 lb
Rear Seat Occupants 350 lb
Fuel 75 gal
Baggage Area 1 80 lb
To determine the loaded weight and CG, follow these steps.
Step 1—List the weight of the aircraft, occupants, fuel, and baggage. Remember, fuel weighs 6 pounds per gallon.
Step 2—Enter the moment for each item listed. Remember “weight x arm = moment.” To simplify calculations, the moments are divided by 100.
Step 3—Total the weight and moments.
Step 4—To determine the CG, divide the moments by the weight.
| NOTE: The weight and balance records for a particular aircraft
will provide the empty weight and moment as well as the information on
the arm distance.
The total loaded weight of 3,330 pounds does not exceed the maximum gross weight of 3,400 pounds and the CG of 84.7 is within the 78-86 inch range; therefore, the aircraft is loaded within limits. |
 |
| Graph Method
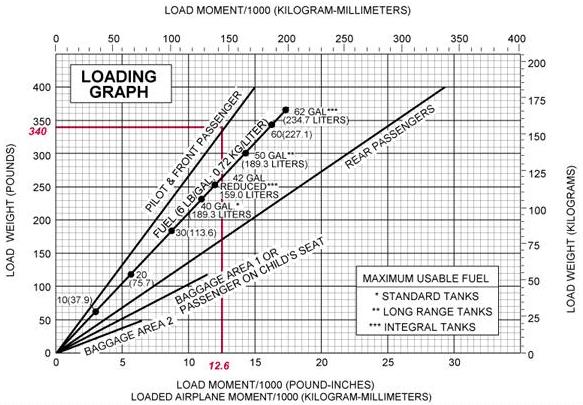
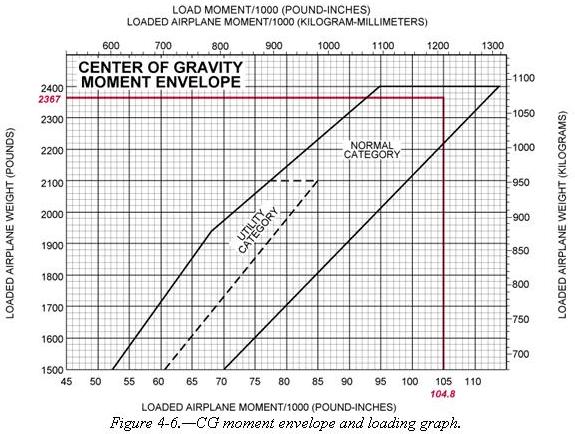
Another method used to determine the loaded weight and CG is the use of graphs provided by the manufacturers. The following is an example of the graph method. [Figures 4-5 and 4-6] Given:
The same steps should be followed as in the computational method except the graphs provided will calculate the moments and allow the pilot to determine if the aircraft is loaded within limits. To determine the moment using the loading graph, find the weight and draw a line straight across until it intercepts the item for which you are calculating the moment. Then draw a line straight down to determine the moment. (The red line on the loading graph represents the moment for the pilot and front passenger. All other moments were determined in the same way.) Once this has been done for each item, total the weight and moments and draw a line for both weight and moment on the center-of-gravity envelope graph. If the lines intersect within the envelope, the aircraft is loaded within limits. In this sample loading problem, the aircraft is loaded within limits. |
 |
 |
 |
 |
 |
Table Method
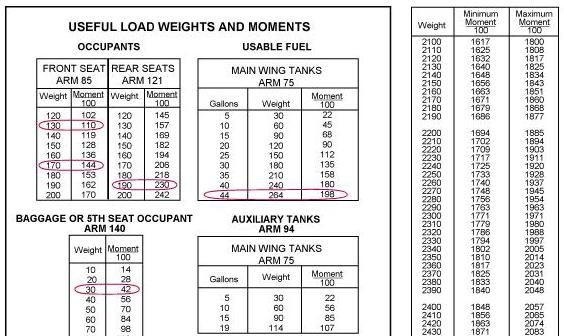
The table method applies the same principles as the computational and graph methods. The information and limitations are contained in tables provided by the manufacturer. Figure 4-7 is an example of a table and a weight and balance calculation based on that table. In this problem, the total weight of 2,799 pounds and moment of 2,278\100 is within the limits of the table.
Shifting, Adding, and Removing Weight
A pilot must be able to accurately and rapidly solve any problems which involve the shift, addition, or removal of weight. For example, the pilot may load the aircraft within the allowable takeoff weight limit, then find a CG limit has been exceeded. The most satisfactory solution to this problem is to shift baggage, passengers, or both. The pilot should be able to determine the minimum load shift needed to make the aircraft safe for flight. Pilots should be able to determine if shifting a load to a new location will correct an out-of-limit condition. There are some standardized calculations which can help make these determinations.
Weight Shifting
When weight is shifted from one location to another, the total weight of the aircraft is unchanged. The total moments, however, do change in relation and proportion to the direction and distance the weight is moved. When weight is moved forward, the total moments decrease; when weight is moved aft, total moments increase. The moment change is proportional to the amount of weight moved. Since many aircraft have forward and aft baggage compartments, weight may be shifted from one to the other to change the CG. If starting with a known aircraft weight, CG, and total moments, calculate the new CG (after the weight shift) by dividing the new total moments by the total aircraft weight.
To determine the new total moments, find out how many moments are gained or lost when the weight is shifted. Assume that 100 pounds has been shifted from station 30 to station 150. This movement increases the total moments of the aircraft by 12,000 lb-in.
Moment when
at station 150 = 100 lb x 150 in = 15,000 lb-in
Moment when
at station 30 = 100 lb x 30 in = 3,000 lb-in
Moment change = 12,000 lb-in
By adding the moment change to the original moment (or subtracting if the weight has been moved forward instead of aft), the new total moments are obtained. Then determine the new CG by dividing the new moments by the total weight:
Total moments = 616,000 + 12,000 = 628,000
CG = 628,000 = 78.5 in
8,000
The shift has caused the CG to shift to station 78.5
A simpler solution may be obtained by using a computer or calculator and a proportional formula. This can be done because the CG will shift a distance which is proportional to the distance the weight is shifted.
Example
Weight Shifted = DCG (change of CG)
Total Weight Distance weight is shifted
100 =
DCG
8,000
120
DCG =
1.5 in
The change of CG is added to (or subtracted from when appropriate)
the original CG to determine the new CG:
77 + 1.5 = 78.5 inches aft of datum
The shifting weight proportion formula can also be used to determine how much weight must be shifted to achieve a particular shift of the CG. The following problem illustrates a solution of this type.
Example
Given:
Aircraft Total Weight 7,800 lb
CG Station 81.5
Aft CG Limit 80.5
Determine how much cargo must be shifted from the aft cargo compartment
at station 150 to the forward cargo compartment at station 30 to move the
CG to exactly the aft limit.
Solution:
Weight to be Shifted =
DCG
Total Weight
Distance Weight Shifted
Weight to be Shifted =
1.0 in
7,800
120 in
Weight to be Shifted = 65 lb
Weight Addition or Removal
In many instances, the weight and balance of the aircraft will be changed by the addition or removal of weight. When this happens, a new CG must be calculated and checked against the limitations to see if the location is acceptable. This type of weight and balance problem is commonly encountered when the aircraft burns fuel in flight, thereby reducing the weight located at the fuel tanks. Most small aircraft are designed with the fuel tanks positioned close to the CG; therefore, the consumption of fuel does not affect the CG to any great extent.
The addition or removal of cargo presents a CG change problem which must be calculated before flight. The problem may always be solved by calculations involving total moments. A typical problem may involve the calculation of a new CG for an aircraft which, when loaded and ready for flight, receives some additional cargo or passengers just before departure time.
Example
Given:
Aircraft Total Weight 6,680 lb
CG Station 80.0
Determine the location of the CG if 140 pounds of baggage is added
to station 150.
{Beginning of page 4-10}
Solution:
Added Weight =
DCG
New Total Weight Distance between weight
and old CG
140
= DCG
6,860 + 140 150 - 80
140
= DCG
7,000
70
CG = 1.4 in aft
Add DCG to old CG
New CG = 80.0 in + 1.4 in = 81.4 in
Example
Given:
Aircraft Total Weight 6,100 lb
CG Station 80.0
Determine the location of the CG if 100 pounds is removed to station
150.
Solution:
Weight Removed = DCG
New Total Weight Distance between
weight and old CG
100
= DCG
6,100 - 100
150 - 78
100
= DCG
6,000
72
CG = 1.2 in forward
Subtract DCG from old CG
New CG = 78 in - 1.2 in = 76.8 in
In the previous examples, the DCG is either added or subtracted
from the old CG. Deciding which to accomplish is best handled by mentally
calculating which way the CG will shift for the particular weight change.
If the CG is shifting aft, the DCG is added to the old CG; if the CG is
shifting forward, the DCG is subtracted from the old CG.