Latitude and Longitude (Meridians and Parallels)
Latitude and Longitude
(Meridians and Parallels)
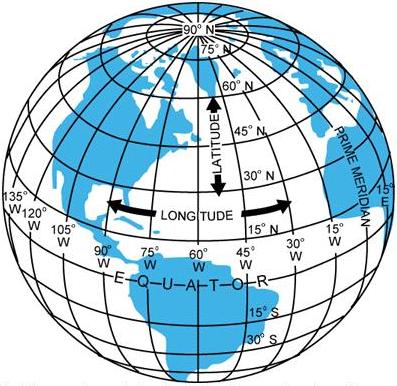
The Equator is an imaginary circle equidistant from the poles
of the Earth. Circles parallel to the Equator (lines running east and west)
are parallels of latitude. They are used to measure degrees of latitude
north or south of the Equator. The angular distance from the Equator to
the pole is one-fourth of a circle or 90°. The 48 conterminous states
of the United States are located between 25° and 49° N. latitude.
The arrows in figure 8-2 labeled “LATITUDE” point to lines of latitude.
Meridians of longitude are drawn from the North Pole to
the South Pole and are at right angles to the Equator. The “Prime Meridian”
which passes through Greenwich, England, is used as the zero line from
which measurements are made in degrees east and west to 180°. The 48
conterminous states of the United States are between 67° and 125°
W. Longitude. The arrows in figure 8-2 labeled “LONGITUDE” point to lines
of longitude.
Any specific geographical point can thus be located by reference
to its longitude and latitude. Washington, DC for example, is approximately
39° N. latitude, 77° W. longitude. Chicago is approximately 42°
N. latitude, 88° W. longitude.
Time Zones
The meridians are also useful for designating time zones. A day
is defined as the time required for the Earth to make one complete revolution
of 360°. Since the day is divided into 24 hours, the Earth revolves
at the rate of 15° an hour. Noon is the time when the Sun is directly
above a meridian; to the west of that meridian is forenoon, to the east
is afternoon. |
|
|
Figure 8-2.—Meridians and parallels—the basis of measuring time,
distance, and direction. |
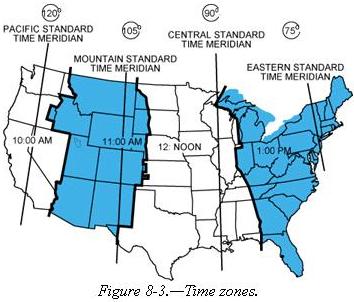
The standard practice is to establish a time zone for each 15° of longitude.
This makes a difference of exactly 1 hour between each zone. In the United
States, there are four time zones. The time zones are Eastern (75°),
Central (90°), Mountain (105°), and Pacific (120°). The dividing
lines are somewhat irregular because communities near the boundaries often
find it more convenient to use time designations of neighboring communities
or trade centers. Figure 8-3 shows the time zones in the United States.
When the Sun is directly above the 90th meridian, it is noon Central Standard
Time. At the same time, it will be 1 p.m. Eastern Standard Time, 11 a.m.
Mountain Standard Time, and 10 a.m. Pacific Standard Time. When “daylight
saving” time is in effect, generally between the last Sunday in April and
the last Sunday in October, the Sun is directly above the 75th meridian
at noon, Central Daylight Time.
These time zone differences must be taken into account during
long flights eastward—especially if the flight must be completed before
dark. Remember, an hour is lost when flying eastward from one time zone
to another, or perhaps even when flying from the western edge to the eastern
edge of the same time zone. Determine the time of sunset at the destination
by consulting the flight service stations (AFSS/FSS) or National Weather
Service and take this into account when planning an eastbound flight.
 |
In most aviation operations, time is expressed in terms of the 24-hour
clock. Air traffic control instructions, weather reports and broadcasts,
and estimated times of arrival are all based on this system. For example:
9 a.m. is expressed as 0900; 1 p.m. is 1300; 10 p.m. is 2200 etc.
Because a pilot may cross several time zones during a flight,
a standard time system has been adopted. It is called Universal Coordinated
Time (UTC) and is often referred to as Zulu time. UTC is the time at the
0° line of longitude which passes through Greenwich, England. All of
the time zones around the world are based on this reference. To convert
to this time, a pilot should do the following:
• Eastern Standard Time Add 5 hours
• Central Standard Time Add 6 hours
• Mountain Standard Time Add 7 hours
• Pacific Standard Time Add 8 hours
For daylight saving time, 1 hour should be subtracted from the
calculated times. |
| Measurement of Direction
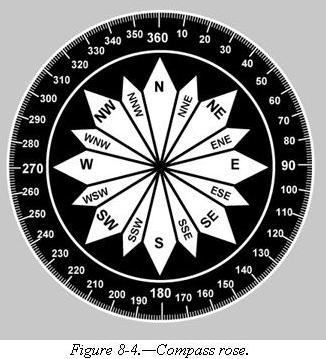
By using the meridians, direction from one point to another can
be measured in degrees, in a clockwise direction from true north. To indicate
a course to be followed in flight, draw a line on the chart from the point
of departure to the destination and measure the angle which this line forms
with a meridian. Direction is expressed in degrees, as shown by the compass
rose in figure 8-4.
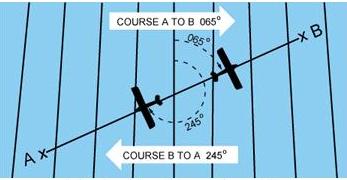
Because meridians converge toward the poles, course measurement should
be taken at a meridian near the midpoint of the course rather than at the
point of departure. The course measured on the chart is known as the true
course. This is the direction measured by reference to a meridian or true
north. It is the direction of intended flight as measured in degrees clockwise
from true north. As shown in figure 8-5, the direction from A to B would
be a true course of 065°, whereas the return trip (called the reciprocal)
would be a true course of 245°. |
|
 |
The true heading is the direction in which the nose of the airplane
points during a flight when measured in degrees clockwise from true north.
Usually, it is necessary to head the airplane in a direction slightly different
from the true course to offset the effect of wind. Consequently, numerical
value of the true heading may not correspond with that of the true course.
This will be discussed more fully in subsequent sections in this chapter.
For the purpose of this discussion, assume a no-wind condition exists under
which heading and course would coincide. Thus, for a true course of 065°,
the true heading would be 065°. To use the compass accurately, however,
corrections must be made for magnetic variation and compass deviation. |
Variation
Variation is the angle between true north and magnetic north.
It is expressed as east variation or west variation depending upon whether
magnetic north (MN) is to the east or west of true north (TN), respectively.
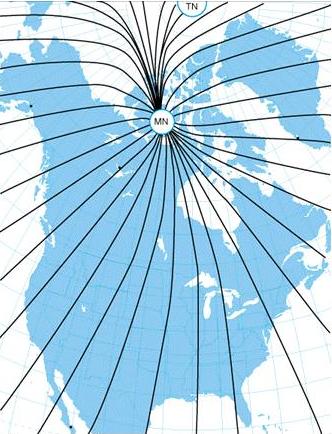
| The north magnetic pole is located close to 71° N. latitude, 96°
W. longitude and is about 1,300 miles from the geographic or true north
pole, as indicated in figure 8-6. If the Earth were uniformly magnetized,
the compass needle would point toward the magnetic pole, in which case
the variation between true north (as shown by the geographical meridians)
and magnetic north (as shown by the magnetic meridians) could be measured
at any intersection of the meridians.
Actually, the Earth is not uniformly magnetized. In the United States
the needle usually points in the general direction of the magnetic pole,
but it may vary in certain geographical localities by many degrees. Consequently,
the exact amount of variation at thousands of selected locations in the
United States has been carefully determined. The amount and the direction
of variation, which change slightly from time to time, are shown on most
aeronautical charts as broken magenta lines, called isogonic lines, which
connects points of equal magnetic variation. (The line connecting points
at which there is no variation between true north and magnetic north is
the isogonic line.) An isogonic chart is shown in figure 8-6. Minor bends
and turns in the isogonic and agonic lines are caused by unusual geological
conditions affecting magnetic forces in these areas. |
|
|
Figure 8-6.—Isogonic chart. Magnetic meridians are in black, geographic
meridians and parallels are in blue. Variation is the angle between a magnetic
and geographic meridian. |
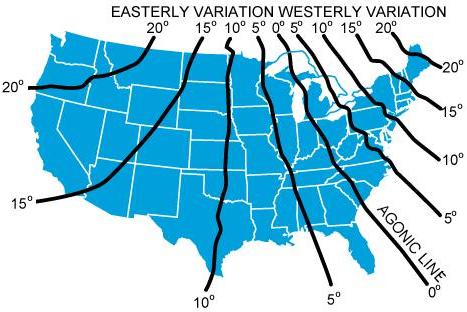 |
On the west coast of the United States, the compass needle points to
the east of true north; on the east coast, the compass needle points to
the west of true north. Zero degree variation exists on the agonic line
which runs roughly through Lake Michigan, the Appalachian Mountains, and
off the coast of Florida, where magnetic north and true north coincide.
[Compare figures 8-7 and 8-8]
Because courses are measured in reference to geographical meridians
which point toward true north, and these courses are maintained by reference
to the compass which points along a magnetic meridian in the general direction
of magnetic north, the true direction must be converted into magnetic direction
for the purpose of flight. This conversion is made by adding or subtracting
the variation which is indicated by the nearest isogonic line on the chart.
The true heading, when corrected for variation, is known as magnetic heading. |
| Figure 8-7.—A typical isogonic chart. The black lines are isogonic
lines which connect geographic points with identical magnetic variation. |
|
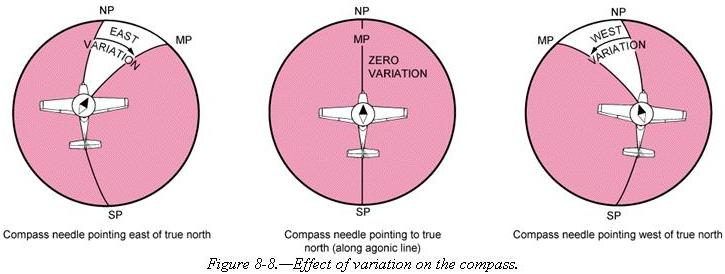 |
If the variation is shown as “9° E,” this means that magnetic north
is 9° east of true north. If a true heading of 360° is to be flown,
9° must be subtracted from 360°, which results in a magnetic heading
of 351°. To fly east, a magnetic heading of 081° (090° - 9°)
would be flown. To fly south, the magnetic heading would be 171° (180°
- 9°). To fly west, it would be 261° (270° - 9°). To fly
a true heading of 060°, a magnetic heading of 051° (060° -
9°) would be flown.
Remember, to convert true course or heading to magnetic course
or heading, note the variation shown by the nearest isogonic line. If variation
is west, add; if east, subtract. One method for remembering whether to
add or subtract variation is the phrase “east is least (subtract) and west
is best (add).”
Deviation
Determining the magnetic heading is an intermediate step necessary to
obtain the correct compass reading for the flight. To determine compass
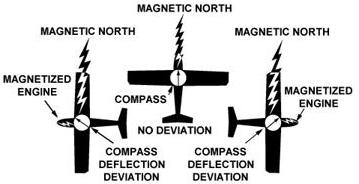
heading, a correction for deviation must be made. Because of magnetic influences
within the airplane such as
| electrical circuits, radio, lights, tools, engine, magnetized metal
parts, etc., the compass needle is frequently deflected from its normal
reading. This deflection is deviation. The deviation is different for each
airplane, and it also may vary for different headings in the same airplane.
For instance, if magnetism in the engine attracts the north end of the
compass, there would be no effect when the plane is on a heading of magnetic
north. On easterly or westerly headings, however, the compass indications
would be in error, as shown in figure 8-9. Magnetic attraction can come
from many other parts of the airplane; the assumption of attraction in
the engine is merely used for the purpose of illustration. |
|
|
Figure 8-9.—Magnetized portions of the airplane cause the compass
to deviate from its normal indications. |
Some adjustment of the compass, referred to as compensation, can be
made to reduce this error, but the remaining correction must be applied
by the pilot.
Proper compensation of the compass is best performed by a competent
technician. Since the magnetic forces within the airplane change, because
of landing shocks, vibration, mechanical work, or changes in equipment,
the pilot should occasionally have the deviation of the compass checked.
The procedure used to check the deviation (called “swinging the compass”)
is briefly outlined.
The airplane is placed on a magnetic compass rose, the engine
started, and electrical devices normally used (such as radio) are turned
on. Tailwheel-type airplanes should be jacked up into flying position.
The airplane is aligned with magnetic north indicated on the compass rose
and the reading shown on the compass is recorded on a deviation card. The
airplane is then aligned at 30° intervals and each reading is recorded.
If the airplane is to be flown at night, the lights are turned on and any
significant changes in the readings are noted. If so, additional entries
are made for use at night.
The accuracy of the compass can also be checked by comparing the
compass reading with the known runway headings.
On the compass card, the letters, N, E, S, and W, are used for
north, east, south, and west. The final zero is omitted from the degree
markings so that figures will be larger and more easily seen.
A deviation card, similar to figure 8-10, is mounted near the
compass, showing the addition or subtraction required to correct for deviation
on various headings, usually at intervals of 30°. For intermediate
readings, the pilot should be able to interpolate mentally with sufficient
accuracy. For example, if the pilot needed the correction for 195°
and noted the correction for 180° to be 0° and for 210° to
be +2°, it could be assumed that the correction for 195° would
be +1°. The magnetic heading, when corrected for deviation, is known
as compass heading.
Figure 8-10.—Compass deviation card.
FOR (MAGNETIC) N 30 60 E 120 150
STEER (COMPASS) 0 28 57 86 117 148
FOR (MAGNETIC) S 210 240 W 300 330
STEER (COMPASS) 180 212 243 274 303 332 |
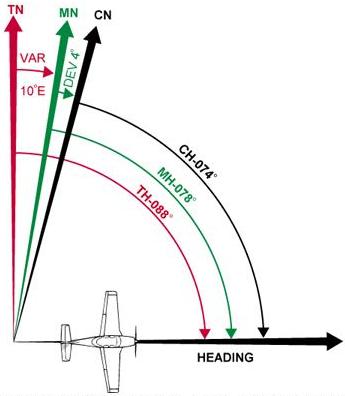
The following method is used by many pilots to determine compass
heading:
After the true course (TC) is measured, and wind correction applied
resulting in a true heading (TH), the sequence TH ± V = MH ±
D = CH is followed to arrive at compass heading. [Figure 8-11]
|
|
|
Figure 8-11.—Relationship between true, magnetic, and compass headings
for a particular instance. |
Home