Before a cross-country flight, a pilot should make common calculations for time, speed, and distance, and the amount of fuel required. These calculations should present no difficulty.
Converting Minutes to Equivalent Hours
It frequently is necessary to convert minutes into equivalent
hours when solving speed, time, and distance problems. To convert minutes
to hours, divide by 60 (60 minutes = 1 hour). Thus, 30 minutes 30/60 =
0.5 hour. To convert hours to minutes, multiply by 60. Thus, 0.75 hour
equals 0.75 x 60 = 45 minutes. Time T = D/GS
{Beginning of page 8-9}
To find the time (T) in flight, divide the distance (D) by the
groundspeed (GS). The time to fly 210 nautical miles at a groundspeed of
140 knots is 210 divided by 140, or 1.5 hours. (The 0.5 hour multiplied
by 60 minutes equal 30 minutes.) Answer: 1:30.
Distance D = GS X T
To find the distance flown in a given time, multiply groundspeed
by time. The distance flown in 1 hour 45 minutes at a groundspeed of 120
knots is 120 x 1.75, or 210 nautical miles.
Groundspeed GS = D/T
To find the groundspeed, divide the distance flown by the time
required. If an airplane flies 270 NM in 3 hours, the groundspeed is 270
divided by 3 = 90 knots.
Converting Knots to Miles Per Hour
Another conversion is that of changing knots to miles per hour. The aviation industry is using knots more frequently than miles per hour, but it might be well to discuss the conversion for those who do use miles per hour when working with speed problems. The National Weather Service reports both surface winds and winds aloft in knots. However, airspeed indicators in some airplanes are calibrated in miles per hour (although many are now calibrated in both miles per hour and knots). Pilots, therefore, should learn to convert windspeeds in knots to miles per hour.
A knot is 1 nautical mile per hour. Because there are 6,076.1 feet in a nautical mile and 5,280 feet in a statute mile, the conversion factor is 1.15. To convert knots to miles per hour, multiply knots by 1.15. For example: a windspeed of 20 knots is equivalent to 23 MPH.
Most flight computers or electronic calculators have a means of making this conversion. Another quick method of conversion is to use the scales of nautical miles and statute miles at the bottom of aeronautical charts.
Fuel Consumption
Airplane fuel consumption rate is computed in gallons per hour. Consequently, to determine the fuel required for a given flight, the time required for the flight must be known. Time in flight multiplied by rate of consumption gives the quantity of fuel required. For example, a flight of 400 NM at a groundspeed of 100 knots requires 4 hours. If the plane consumes 5 gallons an hour, the total consumption will be 4 x 5, or 20 gallons.
The rate of fuel consumption depends on many factors: condition of the engine, propeller pitch, propeller RPM, richness of the mixture, and particularly the percentage of horsepower used for flight at cruising speed. The pilot should know the approximate consumption rate from cruise performance charts, or from experience. In addition to the amount of fuel required for the flight, there should be sufficient fuel for reserve.
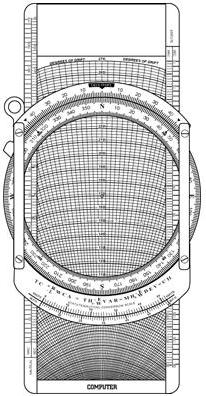
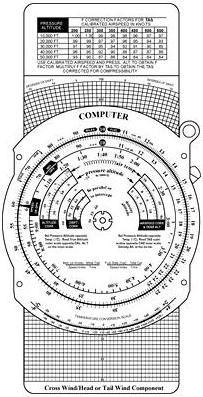
Flight Computers
Up to this point, only mathematical formulas have been used to determine time, distance, speed, fuel consumption, etc. In reality, most pilots will use a mechanical or electronic flight computer. These devices can compute numerous problems associated with flight planning and navigation. The mechanical or electronic computer will have an instruction book and most likely sample problems so the pilot can become familiar with its functions and operation. [Figure 8-16]
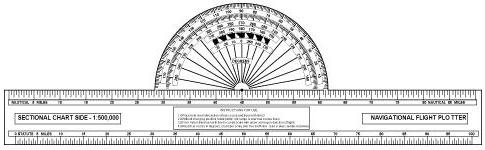
Plotter
Another aid in flight planning is a plotter, which is a protractor and ruler. The pilot can use this when determining true course and measuring distance. Most plotters have a ruler which measures in both nautical and statute miles and has a scale for a sectional chart on one side and a world aeronautical chart on the other. [Figure 8-16]
PILOTAGE
Pilotage is navigation by reference to landmarks or checkpoints.
It is a method of navigation that can be used on any course that has adequate
checkpoints, but it is more commonly used in conjunction with dead reckoning
and VFR radio navigation.
The checkpoints selected should be prominent features common
to the area of the flight. Choose checkpoints that can be readily identified
by other features such as roads, rivers, railroad tracks, lakes, power
lines, etc. If possible, select features that will make useful boundaries
or brackets on each side of the course, such as highways, rivers, railroads,
mountains, etc. A pilot can keep from drifting too far off course by referring
to and not crossing the selected brackets. Never place complete reliance
on any single checkpoint. Choose ample checkpoints. If one is missed, look
for the next one while maintaining the heading. When determining position
from checkpoints, remember that the scale of a sectional chart is 1 inch
= 8 statute miles or 6.86 nautical miles. For example, if a checkpoint
selected was approximately one-half inch from the course line on the chart,
it is 4 statue miles or 3.43 nautical miles from the course on the ground.
In the more congested areas, some of the smaller features are not included
on the chart. If confused, hold the heading. If a turn is made away from
the heading, it will be easy to become lost.
Figure 8-16.—A picture of the computational and wind side of a common mechanical computer, an electronic computer, and plotter.
 |
 |
 |
 |
Roads shown on the chart are primarily the well traveled roads or those most apparent when viewed from the air. New roads and structures are constantly being built, and may not be shown on the chart until the next chart is issued. Some structures, such as antennas may be difficult to see. Sometimes TV antennas are grouped together in an area near a town. They are supported by almost invisible guy wires. Never approach an area of antennas less than 500 feet above the tallest one. Most of the taller structures are marked with strobe lights to make them more visible to a pilot. However, some weather conditions or background lighting may make them difficult to see. Aeronautical charts display the best information available at the time of printing, but a pilot should be cautious for new structures or changes that have occurred since the chart was printed.