
 |
|
||
|
Measurement Systems and Conversions The United States primarily uses the conventional (U.S. or English) system, although it is slowly integrating the metric system (SI). A recommendation to transition to the metric system within ten years was initiated in the 1970s. However, this movement lost momentum, and the United States continues to use both measurement systems. Therefore, information to convert between the conventional (U.S., or English) system and the metric (SI) system has been included in Figure 1-37, Applied Mathematics Formula Sheet, at the end of this chapter. Examples of its use are as follows: 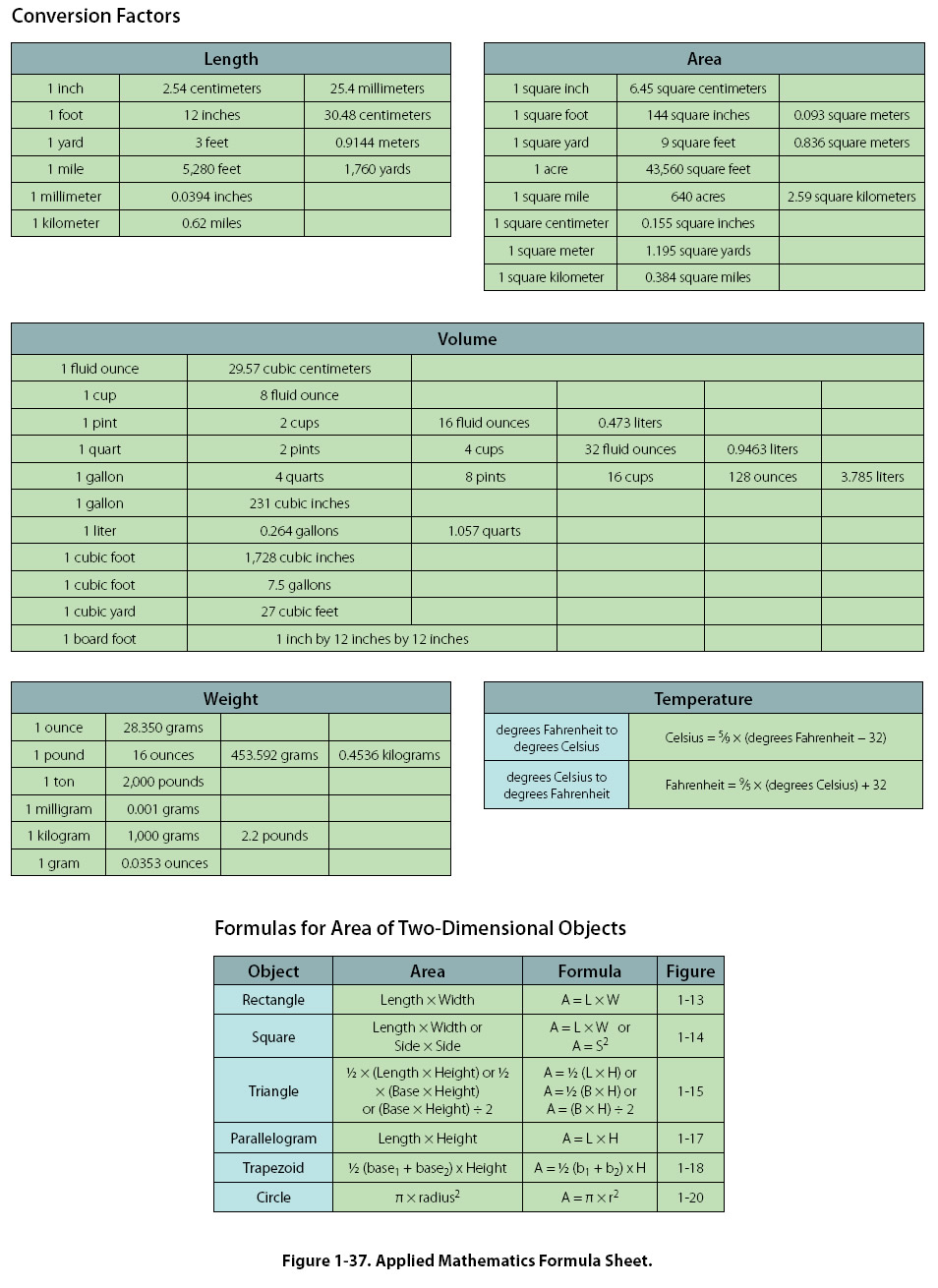
To convert inches to millimeters, multiply the number of inches by 25.4. Example: 20 inches = 20 x 25.4 = 508 mm To convert ounces to grams, multiply the number of ounces by 28.35. Example: 12 ounces = 12 x 28.35 = 340.2 grams The Binary Number System The binary number system has only two digits: 0 and 1. The prefix in the word “binary" is a Latin root for the word “two" and its use was first published in the late 1700s. The use of the binary number system is based on the fact that switches or valves have two states: open or closed (on/off). Currently, one of the primary uses of the binary number system is in computer applications. Information is stored as a series of 0s and 1s, forming strings of binary numbers. An early electronic computer, ENIAC (Electronic Numerical Integrator And Calculator), was built in 1946 at the University of Pennsylvania and contained 17,000 vacuum tubes, along with 70,000 resistors, 10,000 capacitors, 1,500 relays, 6,000 manual switches and 5 million soldered joints. Computers obviously have changed a great deal since then, but are still based on the same binary number system. The binary number system is also useful when working with digital electronics because the two basic conditions of electricity, on and off, can be represented by the two digits of the binary number system. When the system is on, it is represented by the digit 1, and when it is off, it is represented by the digit zero. Place Values The binary number system is a base-2 system. That is, the place values in the binary number system are based on powers of 2. An 8-bit binary number system is shown in Figure 1-34 on the next page.
Converting Binary Numbers to Decimal Numbers To convert a binary number to a decimal number, add up the place values that have a 1 (place values that have a zero do not contribute to the decimal number conversion). Example: Convert the binary number 10110011 to a decimal number. Using the Place Value chart shown in Figure 1-35, add up the place values of the ‘1s’ in the binary number (ignore the place values with a zero in the binary number). The binary number 10110011
|
| ©AvStop Online Magazine Contact Us Return To Books |