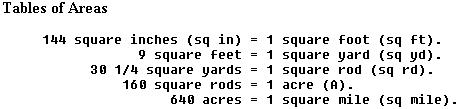
Mensuration formulas deal with the dimensions, areas, and volumes of geometric figures. There are five geometric figures with which you should be familiar, and there is a separate formula for finding the area of each. The area of a plane figure is equal to the number of square units it contains. Areas are measured in different units as compared to measuring length. An area that is square and 1 inch on each side is called a square inch. All area units are square units, such as square inch, square foot, square yard, square rod, and square mile. Other area units are the square centimeter, the square meter, et cetera, found in the metric system of measurement.

The technique for determining the area of any geometric shape is based upon the use of formulas. To solve a problem by formula, it is necessary to -
(1) select the formula that covers the problem situation,
(2) insert the known values in the selected formula, and
(3) then make the necessary mathematical manipulations to find the unknown quantity.
The Rectangle
| A rectangle is a four sided plane figure whose opposite
sides are equal and all of whose angles are right angles (90°). The
rectangle is a very familiar area in mechanics. It is the cross-sectional
area of many beams, rods, fittings, etc. (See figure 1-5.)
The area of a rectangle is the product of the measures of the length and width when they are expressed in the same units of linear measure. The area may be expressed by the formula: |
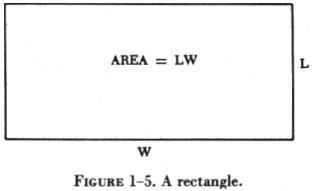 |
where: A = area.
L = length of rectangle.
W = width of rectangle.
EXAMPLE
A certain aircraft panel is in the form of a rectangle having a length of 24 inches and a width of 12 inches. What is the area of the panel expressed in square inches?
FIRST: Determine the known values and substitute them in the formula.
A = L x W
A = 24 x 12
NEXT: Perform the indicated multiplication; the answer will be the total area in square inches.
A = 24 x 12 = 288 sq in
The Square
| A square is a plane figure having four equal sides and four right angles
(figure 1-6).
To determine the area of a square, find the product of the length of any two sides. Since a square is a figure whose sides are equal, the formula can be expressed as the square of the sides or: |
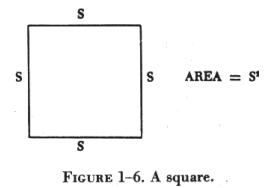 |
where A is the area and S is the length of a side.
EXAMPLE
What is the area of a square plate whose side measures 25 inches?
FIRST: Determine the known value and substitute it in the formula
| A = S2
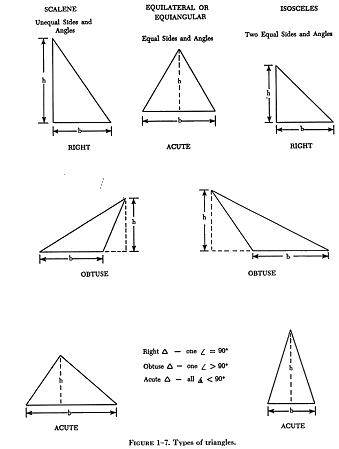
A = 252 NEXT: Perform the indicated multiplication; the answer will be the total area in square inches. A = 25 x 25 = 625 sq in Triangles A triangle is a three sided polygon. There are three basic types of triangle: scalene, equilateral or equiangular, and isosceles. A scalene triangle is one in which all sides and angles are unequal, whereas the equilateral triangle, being just the opposite, has equal sides and equal angles. A triangle that has two equal sides and angles is known as an isosceles triangle. Triangles may be further classified as to right, obtuse, or acute. These terms are descriptive of the included angles of the triangle. A right triangle is one that has one angle measuring 90°. In an obtuse triangle, one angle is greater than 90°, while in an acute triangle all the angles are less than 90°. The various types of triangles are shown in figure 1-7. |
 |
|
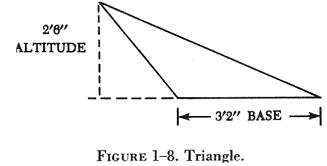
The altitude of a triangle is the perpendicular line drawn from the vertex to the base. In some triangles, as in figure 1-8, it may be necessary to extend the base so that the altitude will meet it. The base of a triangle is the side upon which the triangle is supposed to stand. Any side may be taken as the base. The area of any triangle may be calculated by using the formula: |
 |
A = 1/2 ab
where A is equal to Area; 1/2 is a given constant; a is the altitude
of the triangle; and b is the base.
EXAMPLE
Find the area of the triangle shown in figure 1-8.
FIRST: Substitute the known values in the area formula.
A = 1/2 ab = 1/2 x 2'6" x 3'2"
NEXT: Solve the formula for the unknown value.
A = 1/2 x 30 x 38 = 1140 / 2
A = 570 sq in
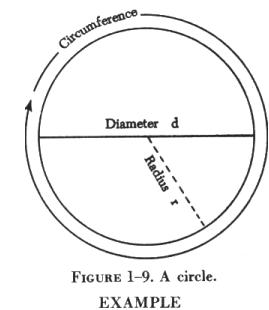
Circumference and Area of a Circle
| To find the circumference (distance around) or the area
of a circle it is necessary to use a number called pi (p). This number
represents the ratio of the circumference to the diameter of any circle.
Pi cannot be found exactly because it is a never ending decimal, but expressed
to four decimal places it is 3.1416, which is accurate enough for most
computations. (See figure 1-9.)
COMPUTING AREA: Circumference of Circles Circumference The circumference of a circle may be found by using the formula: C = where C is the circumference; p is the given constant, 3.1416; and d is the diameter of the circle. |
 |
EXAMPLE
The diameter of a certain piston is 5 inches. What is the circumference of the piston?
FIRST: Substitute the known values in the formula, C = ![]() x d.
x d.
C = 3.1416 x 5
NEXT: Solve the formula for the unknown value.
C = 15.7080 inches.
Area
The area of a circle, as in a rectangle or triangle, must be expressed in square units. The distance that is one-half the diameter of a circle is known as the radius. The area of any circle is found by squaring the radius and multiplying by pi. The formula is expressed thus:
A = ![]() x
r 2
x
r 2
where A is the area of a circle; p is the given constant; and r is the radius of the circle.
EXAMPLE
The bore (inside diameter) of a certain aircraft engine cylinder is 5 inches. Find the cross sectional area of this bore.
FIRST: Substitute the known values in the formula, A = ![]() x r2.
x r2.
A = 3.1416 x 2.52
NEXT: Solve the formula for the unknown value.
A = 3.1416 x 6.25
A = 19.635 sq in
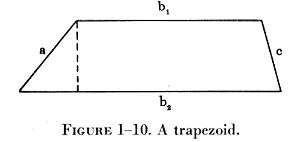
The Trapezoid
| A trapezoid (figure 1-10) is a quadrilateral having one
pair of parallel sides. The area of a trapezoid is determined by using
the formula:
A = 1/2 (b1 + b2)h where A is the area; 1/2 is the given constant; b1 and b2 are the lengths of the two parallel sides; and h is the height. |
 |
EXAMPLE
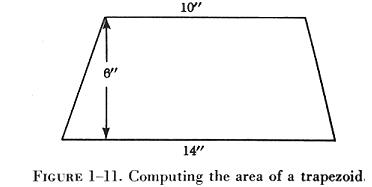
| What is the area of a trapezoid whose bases are 14 inches
and 10 inches, and whose altitude is 6 inches? (See fig. 1-11.)
FIRST: Substitute the known values in the formula. A = 1/2 (b1 + b2)h A = 1/2 (10 + 14)6 NEXT: Solve the formula for the unknown value. A = 1/2 (24)6 A = 1/2 x 144 A = 72 sq in |
 |
Wing Area
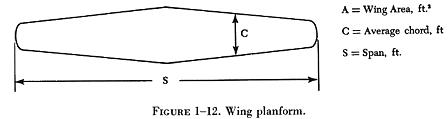 |
To describe the planform of a wing (figure 1-12), several terms are required. To calculate wing area, it will be necessary to consider the meaning of the terms - span and chord. The wing span is the length of the wing from wing tip to wing tip. The chord is the width of the wing from leading edge to trailing edge. If the wing is a tapered wing, the average width or chord, known as the mean chord, must be known in finding the area. The formula for calculating wing area is:
A = SC
where A is the area expressed in square feet, S is the wing span, and C is the average chord.
The process used in calculating wing area will depend upon the shape of the wing. In some instances it will be necessary to use the formula for finding wing area in conjunction with one of the formulas for the area of a quadrilateral or a circle.
EXAMPLES
| 1. Find the area of the wing illustrated in figure 1-13.
To determine the area, it is necessary to decide what formula to use. It can be seen that the wing tips would form a 7 foot diameter circle; the remainder of the wing planform is then in the shape of a rectangle. By combining the formulas for wing area and area of a circle, the area of a wing having circular tips can be calculated. |
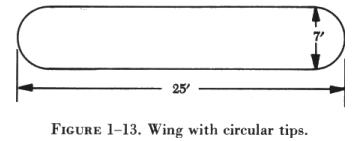 |
FIRST: Substitute the known value in the formula.
A = SC + ![]() R2
R2
A = (25 - 7) (7) + (3.1416) (3.52)
The value for S is represented by the original wing span less the diameter of the circular tips.
NEXT: Solve the formula for the unknown value.
A = (18 x 7) + (3.1416 x 12.25)
A = 126 + 38.5
A = 164.5 sq ft
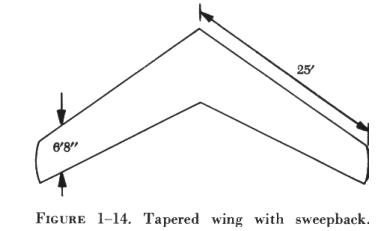
| 2. Find the area of a tapered wing (figure 1-14) whose
structural span is 50 feet and whose mean chord is 6'8".
FIRST: Substitute the known values in the formula. A = SC A = 50' x 6'8". NEXT: Solve the formula for the unknown value. A = 50' x 6.67' A = 333.5 sq ft |
 |
3. Find the area of a trapezoidal wing (shown in figure 1-15) whose leading edge span measures 30 feet, whose trailing edge span measures 34 feet, and whose chord is 5 feet.
FIRST: Substitute the known values in the formula.
A = 1/2 (b1 + b2)h
A = 1/2 (30 + 34)5
NEXT: Solve the formula for the unknown value.
A = 1/2 (64) 5
A = 1/2 (320)
A = 160 sq ft