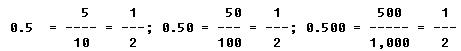
Decimals are fractions whose denominators are 10 or some multiple of 10, such as 100, 1,000, 10,000, etc. They are indicated by writing one or more digits to the right of a reference mark called a decimal point. Thus:
6
---- = 0.6, both read six tenths.
10
6
----- = 0.06, both read six hundredths.
100
6
----- = 0.006, both read six thousandths.
1,000
When writing a decimal, any number of zeros may be written at the right end without changing the value of the decimal. This may be illustrated in the following manner:
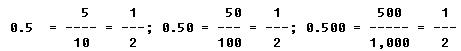
A decimal fraction that is written where there is no whole number as 0.6, 0.06, etc., is called a pure decimal. When a whole number and a decimal fraction are written together as 3.6, 12.2, 131.12, etc., the number is known as a mixed decimal.
Addition of Decimals
When computing decimals, the rule of likeness requires that we add or
subtract only like denominations. This rule was discussed previously under
addition and subtraction of whole numbers. To add or subtract decimal expressions,
arrange the decimals so that the decimal points align vertically, and add
or subtract as with integers. Place the decimal point in the result directly
below the decimal points in the addends or minuend and subtrahend.
| EXAMPLES
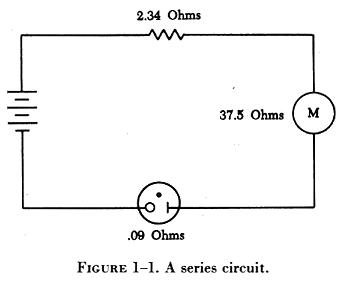
The total resistance of series circuit (figure 1-1) is equal to the
sum of the individual resistances. What is the total resistance for the
diagram shown in this example?
FIRST: Arrange the decimals in a vertical column so that the decimal points are in alignment. |
 |
NEXT: Complete the addition following the technique used in adding whole numbers. Place the decimal point in the result directly below the other decimal points.
2.34
37.5
0.09
-----
39.93 ohms
Subtraction of Decimals
A series circuit containing two resistors has a total resistance of 37.27 ohms. One of the resistors has a value of 14.88 ohms. What is the value of the remaining resistor?
FIRST: Arrange the decimals in a vertical column so that the decimal points are in alignment.
37.27
- 14.88
-----
NEXT: Perform the subtraction process using the procedure for subtracting whole numbers. Place the decimal point in the result directly below the other decimal points.
37.27
- 14.88
-----
22.39 ohms
Multiplication of Decimals
The multiplication of a decimal by another decimal will always produce an answer smaller than either of the two numbers. When a decimal is multiplied by a whole number or by a mixed decimal, the answer will lie between the two numbers.
When multiplying a decimal fraction by an integer or another decimal, establishing the position of the decimal point in the product causes the greatest amount of difficulty. To multiply decimals, ignore the decimal points and multiply the terms as though they were whole numbers. To locate the decimal point in the product, begin at the right of the product and point off toward the left the number of decimal places that will equal the sum of the decimal places in the quantities multiplied.
EXAMPLE
Using the formula, Watts = Amperes x Voltage, what is the wattage of an electric heater that uses 9.45 amperes from a 120 volt source?
FIRST: Arrange the terms and multiply. Ignore the decimal point.

NEXT: Locate the decimal point. Begin at the right of the product and point off toward the left the number of places that will equal the sum of the decimal places in the quantities multiplied.

In some problems the number of digits in the product will be less than the sum of the decimal places in the quantities multiplied. Where this occurs, merely add zeros to the left of the product until the number of digits equals the sum of the decimal places in the quantities multiplied.
EXAMPLE
Multiply 0.218 by 0.203.
FIRST: Arrange the terms and multiply, ignoring the decimal point.

NEXT: Locate the decimal point. Add a zero to the left of the product so that the number of places will equal the sum of the decimal places in the quantities multiplied.

Division of Decimals
When one or both of the terms of a division problem involve decimal expressions, the quotient is found by converting the problem to one involving a whole number.
Two facts relating to division of decimals that must be borne in mind are: (1) When the dividend and divisor are multiplied by the same number, the quotient remains unchanged; and (2) if the divisor is a whole number, the decimal place in the quotient will align vertically with the decimal in the dividend when the problem is expressed in long division form.
To divide decimal expressions, count off to the right of the decimal
point in the dividend the same number of places that are located to the
right of the decimal point in the divisor. Insert a caret ( ^ ) to the
right of the last digit counted. If the number of decimal places in the
dividend is less than the number of decimal places in the divisor, add
zeros to the dividend, remembering that there must be at least as many
decimal places in the dividend as in the divisor. Divide the terms, disregarding
the decimal points entirely. Place the decimal point in the quotient so
that it aligns vertically with the caret mark in the dividend.
EXAMPLE
The wing area of a certain airplane is 245 square feet; its span is 40.33 feet. What is the mean chord of its wings?
FIRST: Arrange the terms as in long division and move the decimal point to the right, adding zeros as necessary, and insert a caret.
![]()
NEXT: Divide the terms, disregarding the decimal points entirely. Add additional zeros to the right to permit carrying the quotient to the desired accuracy.
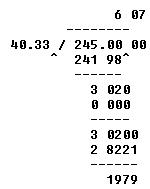
THEN: Place the decimal point in the quotient so that it aligns vertically with the caret mark in the dividend.

Rounding Off Decimals
There is a general tendency to think of all numbers as being precise. Actually the whole realm of measurement involves numbers that are only approximations of precise numbers. For example, measurements of length, area, and volume are at best approximations. The degree of accuracy, of these measurements depends on the refinement of the measuring instruments.
Occasionally it is necessary to round a number to some value that is practical to use. For example, a measurement is computed to be 29.4948 inches. It is impractical, if not impossible, to measure this accurately with a steel rule which is accurate only to 1/64 of an inch.
To use this measurement, we can use the process of "rounding." A decimal expression is "rounded off" by retaining the digits for a certain number of places and discarding the rest. The retained number is an approximation of the computed or exact number. The degree of accuracy desired determines the number of digits to be retained. When the digit immediately to the right of the last retained digit is a 5, or greater than 5, increase the last retained digit by 1. When the digit immediately to the right of the last retained digit is less than 5, leave the last retained digit unchanged.
EXAMPLE
Round 29.4948 to the nearest tenth.
FIRST: Determine the number of digits to retain. In this case one-tenth being the first place to the right of the decimal point.
29.4948
NEXT: Change the value of the last retained digit, if required. In this case, since 9 is greater than 5, the final decimal is expressed thus:
29.4948 becomes 29.5 inches.
Converting Decimals to Common Fractions
To change a decimal fraction to a common fraction, count the number of digits to the right of the decimal point. Express the number as the numerator of a fraction whose denominator is 1 followed by the number of zeros that will equal the number of digits to the right of the decimal point.
EXAMPLE
Express 0.375 as a common fraction.
FIRST: Count the number of digits to the right of the decimal point.
. 3 7 5
1 2 3
NEXT: Express the number as the numerator of a fraction whose denominator is 1 followed by the number of zeros that will equal the number of digits to the right of the decimal point.
![]()
Many times a dimension appearing in a maintenance manual or on a blueprint is expressed in decimal fractions. In order to use the dimension, it must be converted to some equivalent approximation applicable to the available measuring device. From the mechanic's standpoint, the steel rule will be the device most frequently used.
To change a decimal to the nearest equivalent fraction having a desired denominator, multiply the decimal by the desired denominator. The result will be the numerator of the desired fraction.
EXAMPLE
When accurate holes of uniform diameter are required, they are first drilled 1/64 inch undersize and reamed to the desired diameter. What size drill would be used before reaming a hole to 0.763?
FIRST: Multiply the decimal by the desired denominator of 64.

NEXT: Round the product to a whole number and express it as the numerator of the desired denominator.
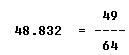
THEN: To determine the drill size, subtract 1/64 inch from the finished hole size.
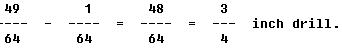
Converting Common Fractions to Decimals
To convert a common fraction, whether proper or improper, to a decimal,
divide the numerator by the denominator. Add zeros to the right to permit
carrying the quotient to the desired accuracy.
 |
EXAMPLE
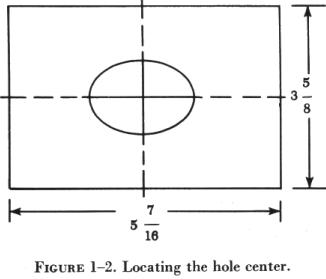
Find the distance the center of the hole (figure 1-2) is from the plate edges when the center of the hole is in the center of the plate. Express the length and width of the plate in decimal forms, and then divide each by 2. Express the final result to the nearest 32nd. FIRST: Change the mixed numbers to improper fractions.
|
NEXT: Convert the improper fractions to decimal expressions.
![]()
THEN: Divide the decimal expressions by 2 to find the center of the plate.

FINALLY: Express the final results to the nearest 32nd.
