A fraction is an indicated division that expresses one or more of the equal parts into which a unit is divided. For example, the fraction 2/3 indicates that the whole has been divided into 3 equal parts and that 2 of these parts are being used or considered. The number above the line is the numerator; and the number below the line is the denominator.
If the numerator of a fraction is equal to or larger than the denominator, the fraction is known as an improper fraction. In the fraction 15/8, if the indicated division is performed, the improper fraction is changed to a mixed number, which is a whole number and a fraction:
15 7
---- = 1 ---
8
8
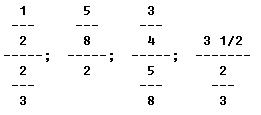
A complex fraction is one that contains one or more fractions or mixed numbers in either the numerator or denominator. The following fractions are examples:

A decimal fraction is obtained by dividing the numerator of a fraction by the denominator and showing the quotient as a decimal. The fraction equals 5/8 = 0.625.
A fraction does not change its value if both numerator and denominator
are multiplied or divided by the same number.
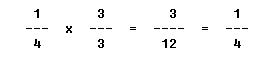
The same fundamental operations performed with whole numbers can also be performed with fractions. These are addition, subtraction, multiplication, and division.
Addition and Subtraction of Common Fractions
In order to add or subtract fractions, all the denominators must be alike. In working with fractions, as in whole numbers, the rule of likeness applies. That is, only like fractions may be added or subtracted.
When adding or subtracting fractions that have like denominators, it is only necessary to add or subtract the numerators and express the result as the numerator of a fraction whose denominator is the common denominator. When the denominators are unlike, it is necessary to first reduce the fractions to a common denominator before proceeding with the addition or subtraction process.
EXAMPLES
1. A certain switch installation requires 5/8 inch plunger travel before switch actuation occurs. If 1/8 inch travel is required after actuation, what will be the total plunger travel?
FIRST: Add the numerators.
5 + 1 = 6
NEXT: Express the result as the numerator of a fraction whose denominator is the common denominator.
![]()
2. The total travel of a jackscrew is 13/16 of an inch. If the travel in one direction from the neutral position is 7/16 of an inch, what is the travel in the opposite direction?
FIRST: Subtract the numerators.
13 - 7 = 6
NEXT: Express the result as the numerator of a fraction whose denominator is the common denominator.
![]()
3. Find the outside diameter of a section of tubing that has a 1/4 inch inside diameter and a combined wall thickness of 5/8 inch.
FIRST: Reduce the fractions to a common denominator.
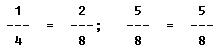
NEXT: Add the numerators, and express the result as the numerator of a fraction whose denominator is the common denominator.
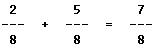
4. The tolerance for rigging the aileron droop of an airplane is 7/8 inch plus or minus 1/5 inch. What is the minimum droop to which the aileron can be rigged?
FIRST: Reduce the fractions to a common denominator.
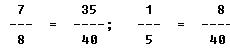
NEXT: Subtract the numerators, and express the result as in the above examples.
![]()
Finding the Least Common Denominator
When the denominators of fractions to be added or subtracted are such that a common denominator cannot be determined readily, the LCD (least common denominator) can be found by the continued division method.
To find the LCD of a group of fractions, write the denominators in a horizontal row. Next, divide the denominators in this row by the smallest integer that will exactly divide two or more of the denominators. Bring down to a new row all the quotients and numbers that were not divisible. Continue this process until there are no two numbers in the resulting row that are divisible by any integer other than one. Multiply together all the divisors and the remaining terms in the last row to obtain the least common denominator.
EXAMPLE
What is the LCD for 7/8, 11/20, 8/36, 21/45?
FIRST: Write the denominators in a horizontal row and divide this row by the smallest integer that will exactly divide two or more of the numbers.
![]()
NEXT: Continue this process until there are no two numbers in the resulting row that are divisible by any integer other than one.

THEN: Multiply together all the divisors and remaining terms in the last row to obtain the LCD.
LCD = 2 x 2 x 3 x 3 x 5 x 2 = 360
Multiplication of Fractions
The product of two or more fractions is obtained by multiplying the numerators to form the numerator of the product and by multiplying the denominators to form the denominator of the product. The resulting fraction is then reduced to its lowest terms. A common denominator need not be found for this operation, as the new denominator in most cases will be different from that of all the original fractions.
EXAMPLE
What is the product of 3/5 x 12/22 x 1/2?
FIRST: Multiply the numerators together.
3 x 12 x 1 = 36
NEXT: Multiply the denominators together.
5 x 22 x 2 = 220
THEN: Reduce the resulting fraction to its lowest terms.
![]()
Cancellation
Cancellation is a technique of dividing out or canceling all common factors that exist between numerators and denominators. This aids in locating the ultimate product by eliminating much of the burdensome multiplication.
EXAMPLE
What is the product of 18/10 x 5/3?
The product could be found by multiplying 18 x 5 and 10 x 3, then dividing the product of the numerators by the product of the denominators. However, a much easier method of solution is by cancellation. It is apparent that the 10 in the denominator and the 5 in the numerator can both be divided an exact number of times by 5.
![]()
Also, the 18 and 3 are both exactly divisible by 3.
![]()
The resulting 6 in the numerator and the 2 in the denominator are both divisible by 2.
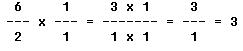
The fraction is thus reduced to its lowest terms, and the final multiplication and division steps are performed with ease when compared with the task of multiplying and dividing the larger fractions.
Division of Common Fractions
The division of common fractions is accomplished most conveniently by converting the problem into a multiplication of two common fractions. To divide one fraction by another fraction, invert the divisor fraction and multiply the numerators together and the denominators together. This is known as the inverted divisor method. Always keep in mind the order in which the fractions are written. It is important in division that the operations be performed in the order indicated. Also, remember that it is always the divisor that is inverted, never the dividend.