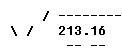
Power
When one number, the base, is used as a factor two or more times, the result is a power of the base. A positive integral exponent, written as a small number just to the right, and slightly above the base number, indicates the number of times the base is used as a factor.
Thus, 4 squared, or 42 means 4 x 4, which is 16. The 4 is the base, the 2 is the exponent, and the 16 is the power.
Roots
A root of a number is one of two or more equal numbers that, when multiplied together, will produce the number. Such a number is called an equal factor. Thus, two equal factors that will produce 9 when multiplied together are 3 and 3. Therefore, the square root of 9 equals 3. This may be written (sqrt) 9 = 3. The symbol is called a radical sign. Another method of indicating the square root of a number is to use a fractional exponent such as 91/2 = 3. If the root to be taken is other than a square root, it may be shown in a similar manner; that is, the cube root of 9 may be written 91/3. For example, the cube root of 8 equals 2 and may be written (cube root) 8 = 2, or 81/3 = 2; the fourth root of 256 equals 4 and may be written (forth root) 256 = 4, or 2561/4 = 4.
Computation of Square Root
It is comparatively easy to determine the square root of such numbers as 4, 9, 16, and 144. The numbers are the perfect squares of small numbers. Unfortunately, all numbers are not perfect squares; neither are they small. The square of a number is the product of that number multiplied by itself. Extracting the square root of a number is the reverse process of squaring a number, and is essentially a special division process. A description of this process follows and is presented in example form.
EXAMPLE
Find the square root of 213.16
FIRST: Starting at the decimal point, and marking off in both directions from the decimal point, separate the number into periods of two figures each. The last period at the left end need not have two figures; all others must have two figures. A zero may be added to the right end so that the period will have two figures.
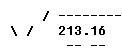
NEXT: Select the largest number that can be squared in the first period. Place the selected number above the radical sign, and place the square of this number under the first period and subtract.

THEN: Bring down the next pair.
(1) Multiply the root by 2 and place the product to the left of the remainder as the trial divisor.
(2) Determine the number of times the trial divisor will go into that portion of the remainder that is one digit more than the trial divisor. Write this number to the right of the digit in the trial divisor to form the final divisor and also to the right of the digit in the root.
(3) Multiply this number times the completed divisor. If the resulting product is larger than the remainder, reduce the number by one, both in the root and in the final divisor, and repeat the multiplication process.
(4) Subtract the product formed from the remainder and bring down the next pair to form a new remainder.
(5) To complete the solution of extracting the square root, simply repeat the procedure set forth in this step for each period of numbers remaining. It is unnecessary to carry the root beyond the number of digits possessed by the original number.

Two will divide into 11, 5 times. However, 5 x 25 is greater than 113, so the 5 must be reduced to a 4.
The decimal is placed in the root so that the number of digits in the
whole number portion of the root is equal to the sum of the periods, or
pairs, in the whole number portion of the number from which the root was
extracted.
| Powers of Ten
The difficulty of performing mathematical problems with very large (or very small) numbers and the counting and writing of many decimal places are both an annoyance and a source of error. The problems of representation and calculation are simplified by the use, of "powers of ten." (See figure 1-4.). This system, sometimes referred to as "Engineer's Shorthand," requires an understanding of the principles of the exponent. These are summarized as follows: (1) The positive exponent (or power) of a number is a shorthand method of indicating how many times the number is multiplied by itself. For example, 23 (read as 2 cubed or 2 to the third power) means 2 is to be multiplied by itself 3 times: 2 x 2 x 2 = 8. A number with a negative exponent may be defined as its inverse or reciprocal (1 divided by the number) with the same exponent made positive. For example, 2-3 (read as 2 to the minus 3 power) is the same as |
 |

(2) Any number, except zero, to the zero power is equal to 1. When a number is written without an exponent, the value of the exponent is 1. When an exponent has no sign (+ or -) preceding it, the exponent is positive.
(3) The value of a number does not change when it is both multiplied and divided by the same factor (5 x 10 divided by 10 = 5). Moving the decimal point of a number to the left is the same as dividing the number by 10 for each place the decimal point moves. Conversely, moving the decimal point to the right is the same as multiplying the number by 10 for each place the decimal point moves.
The procedure for use of powers of ten may be summarized as follows:
(1) Move the decimal point to the place desired. Count the number of places the decimal point is moved.
(2) Multiply the altered number by 10 to a power equal to the number of places the decimal point was moved.
(3) The exponent of 10 is negative if the decimal point is moved to the right, and it is positive if the decimal point is moved to the left.
An aid for remembering the sign to be used is: L, A, R, D. When the decimal point moves Left, you Add; and when the decimal point moves Right, you Deduct.
In most instances, you will find it convenient to reduce the numbers used to numbers between 1 and 10 times 10 to the proper power. Unless otherwise specified, all answers to problems using powers of ten will conform to that requirement.
Powers of Ten Added and Subtracted
Before using powers of ten in mathematical operations, it will be beneficial to review a few more principles governing exponents:
If two or more numbers are written with the same base, their product is equal to the base raised to a power equal to the algebraic sum of their exponents.
![]()
If two numbers are written with the same base, their quotient is equal to the base raised to a power equal to the algebraic difference of their exponents (numerator's exponent minus denominator's exponent).
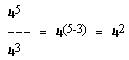
A factor may be moved from numerator to denominator or from denominator to numerator by changing the sign of its exponent. Thus we have
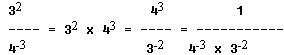
The bases must be the same before numbers can be multiplied or divided by the addition or subtraction of their exponents. Thus, a5 x b6 cannot be combined because the bases (a and b) are not the same.
Note particularly that the rules specify algebraic addition and algebraic subtraction of the powers. Here are some summarizing examples:
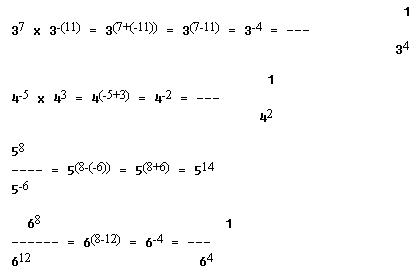
Multiplication and division employing powers of ten may be performed in three simple steps as follows:
(1) Reduce all numbers to values between 1 and 10 multiplied by 10 to the proper power.
(2) Perform the indicated operations.
(3) Change the result to a number between 1 to 10 multiplied by 10 multiplied by 10 to the proper power.