An important application of the common fraction is that of ratio. A ratio represents the comparison of one number to another number. Comparison by the use of ratios has widespread application in the field of aviation. A ratio is used to express the comparison of the volume of a cylinder when the piston is at bottom center to the volume of a cylinder when the piston is at top center. This is referred to as the compression ratio. The aspect ratio of an aircraft wing is a comparison of the wing span to the wing chord. The relationship of maximum speed, wing area, wing span, loaded weight, and horsepower of different makes and models of aircraft may be compared through the use of ratios.
A ratio is the quotient of one number divided by another number, expressed in like terms. A ratio, therefore, is the fractional part that one number is of another. A ratio may be expressed as a fraction, or it may be written using the colon (:) as the symbol for expressing ratio; thus the ratio 7/8 can be written 7:8.
Finding the Ratio of Two Quantities
To find a ratio, the first term is divided by the second term. Both quantities of both terms must be expressed in the same units, and reduced to their lowest terms.
EXAMPLES
1. What is the weight ratio of a fuel load of 800 gallons to one of 10,080 pounds? Assume that the fuel weighs 7.2 pounds per gallon.
FIRST: Express the fuel load in gallons as the numerator of a fraction whose denominator is the fuel load in pounds.
800 gal.
R = ----------
10,080 lb
NEXT: Express both quantities in the same unit (pounds).
(800 x 7.2)
lb
R = ---------------
10,080 lb
THEN: Perform the indicated mathematical manipulations and reduce to lowest terms.
![]()
What is the ratio in gallons?
FIRST: Express the ratio in fractional form.
800 gal.
R = ----------
10,080 lb
NEXT: Express both quantities in the same unit (gallons).
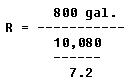
THEN: Perform the indicated mathematical manipulations and reduce to lowest terms.
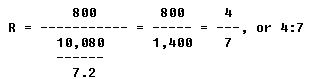
2. If the cruising speed of an airplane is 200 knots and its maximum speed is 250 knots, what is the ratio of cruising speed to maximum speed?
FIRST: Express the cruising speed as the numerator of a fraction whose denominator is the maximum speed.
200
R = -----
250
NEXT: Reduce the resulting fraction to its lowest terms.
![]()
THEN: Express the result as a ratio of one.
![]()
Finding the Quantity of the First Term
Now consider the situation when the ratio and the quantity that corresponds to the second term are given, and it is required to find the quantity that corresponds to the first term. To solve this type problem, multiply the term that corresponds to the second term by the fraction that represents the ratio.
EXAMPLE
The given ratio is 5/7 and the quantity that corresponds to the second term is 35. Find the quantity that corresponds to the first term.
FIRST: Express the problem as the product of the second term times the ratio.
35 x 5/7 =
NEXT: Perform the indicated operation.
35 x 5/7 = 5 x 5/1 = 25
The first term is 25. The proof of this can be demonstrated by showing that the ratio of 25 to 35 is 5:7, reduced to lowest terms.
25/35 = 5/7
Finding the Quantity of the Second Term
To solve a problem of this type, the ratio of the two quantities and the quantity that corresponds to the first term must be known. The solution is obtained by dividing the known number by the fraction that represents the ratio.
EXAMPLE
The ratio of two quantities is 2/3; the quantity that corresponds to the first term is 100. Find the quantity that corresponds to the second term.
FIRST: Express the problem as the quotient of the first term divided by the ratio.
100 divided by 2/3 =
NEXT: Perform the indicated operation.
100 divided by 2/3 = 100 x 3/2 = 50 x 3/1 = 150
The second term is 150. Again, this can be proved by expressing 100 as a ratio of 150.
100/150 = 2/3