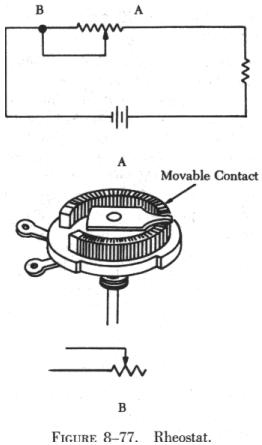
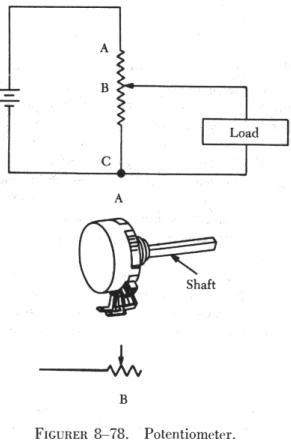
| Rheostats and potentiometers are constructed of a circular resistance
material over which a sliding contact moves. The resistance may be distributed
in many ways, and the method used determines the classification as either
linear or tapered. The linear type provides a resistance evenly distributed
over its entire length, while the tapered has more resistance per unit
length at one end than at the other. As an example, a one-half turn of
a linear rheostat places one half of the total resistance between either
end and the slider, while a one-half turn of a tapered rheostat places
one-tenth (or any desired fraction) of the total resistance between one
end and the slider.
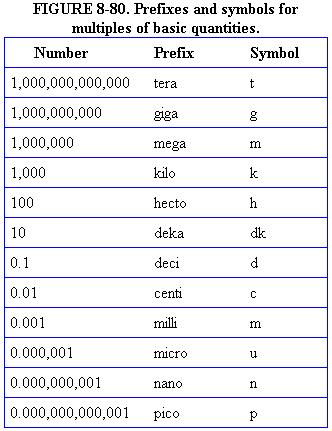
Prefixes
In any system of measurements, a single set of units is usually not
sufficient for all the computations involved in electrical repair and maintenance.
Small distances, for example, can usually be measured in inches, but larger
distances are more meaningfully expressed in feet, yards, or miles. Since
electrical values often vary from numbers that are a millionth part of
a basic unit of measurement to very large values, it is often necessary
to use a wide range of numbers to represent the values of such units as
volts, amperes, or ohms. A series of prefixes which appear with the name
of the unit have been devised for the various multiples or submultiples
of the basic units. There are 12 of these prefixes, which are also known
as conversion factors. Six of the most commonly used prefixes with a short
definition of each are as follows: |
FIGURE 8-79. Conversion Table.
1 ampere = 1,000,000 microamperes.
1 ampere = 1,000 milliamperes.
1 farad = 1,000,000,000,000 micromicrofarads.
1 farad = 1,000,000 microfarads.
1 farad = 1,000 millifarads
1 kilowatt = 1,000 watts.
1 megohm = 1,000,000 ohms.
1 microampere = .000001 ampere.
1 microfarad = .000001 farad.
1 microhm = .000001 ohm
1 microvolt = .000001 volt
1 microwatt = .000001 watt.
1 micromicrofarad = .000000000001 farad.
1 milliampere = .001 ampere.
1 millihenry = .001 henry.
1 millimho = .001 mho.
1 milliohm. = .001 ohm.
1 millivolt = .001 volt.
1 milliwatt = .001 watt.
1 volt = 1,000,000 microvolts.
1 volt = 1,000 millivolts.
1 watt = 1,000 milliwatts.
1 watt = .001 kilowatt.
|