Sound has been defined as a series of disturbances in matter that the human car can detect. This definition can also be applied to disturbances which are beyond the range of human hearing.
There are three elements which are necessary for the transmission and reception of sound. These are the source, a medium for carrying the sound, and the detector. Anything which moves back and forth (vibrates) and disturbs the medium around it may be considered a sound source.
An example of the production and transmission of sound is the ring of a bell. When the bell is struck and begins to vibrate, the particles of the medium (the surrounding air) in contact with the bell also vibrate. The vibrational disturbance is transmitted from one particle of the medium to the next, and the vibrations travel in a "wave" through the medium until they reach the ear. The eardrum, acting as detector, is set in motion by the vibrating particles of air, and the brain interprets the eardrum's vibrations as the characteristic sound associated with a bell.
Wave Motion
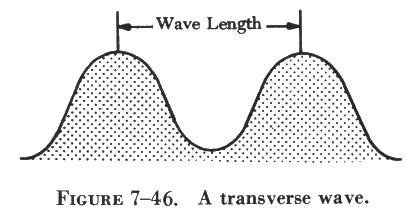
| Since sound is a wave motion in matter, it can best be understood by first considering water waves. When a stone is thrown into a pool, a series of circular waves travel away from the disturbance. In figure 7-46 such waves are diagramed as though seen in cross section, from the side. Notice that water waves are a succession of crests and troughs. The wavelength is the distance from the crest of one wave to the crest of the next. Water waves are known as transverse waves because the motion of the water molecules is up and down, or at right angles to the direction in which the waves are traveling. This can be seen by observing a cork on the water, bobbing up and down as the waves pass by; the corks moves very little from side to side. |  |
Sound travels through matter in the form of longitudinal wave motions. These waves are called longitudinal waves because the particles of the medium vibrate back and forth longitudinally in the direction of propagation, as shown in figure 7-47.
When the tine of a tuning fork (figure 7-47) moves in an outward direction, the air immediately in front of the tine is compressed so that its momentary pressure is raised above that at other points in the surrounding medium. Because air is elastic, this disturbance is transmitted progressively in an outward direction from the tine in the form of a compression wave.
When the tine returns and moves in an inward direction, the air in front of the tine is rarefied so that its momentary pressure is reduced below that at other points in the surrounding medium. This disturbance is transmitted in the form of a rarefaction (expansion) wave and follows the compression wave through the medium.
The progress of any wave involves two distinct motions: (1) The wave itself moves forward with constant speed, and (2) simultaneously, the particles of the medium that convey the wave vibrate harmonically. (Examples of harmonic motion are the motion of a clock pendulum, the balance wheel in a watch, and the piston in a reciprocating engine.)
The period of a vibrating particle is the time "t" (in seconds) required for the particle to complete one vibration.
The frequency "f" is the number of vibrations completed per second and may be expressed in cps. When expressed in this unit, the word "cycles" means vibrations. The period is the reciprocal of the frequency:
t = 1/f.
The velocity of a wave is equal to the wavelength ![]() (lambda) divided by the period. Since the period is the reciprocal of the
frequency, the velocity is,
(lambda) divided by the period. Since the period is the reciprocal of the
frequency, the velocity is,
v = f![]()
where:
v = velocity in ft/sec
f = frequency in cps
![]() = wavelength in ft
= wavelength in ft
The amplitude of vibration is the maximum displacement of the particle from its equilibrium position.
Two particles are in phase when they are vibrating with the same frequency, and continually pass through corresponding points of their paths at the same time. For any other condition the particles are out of phase. The two particles are in phase opposition when they reach their maximum displacement in opposite directions at the same time.
The wavelength is the distance measured along the direction of propagation between two corresponding points of equal intensity that are in phase on adjacent waves. This length can be represented by the distance between the adjacent maximum rarefaction points in the traveling sound wave (figure 7-47). When referring to figure 7-47, keep in mind that the transverse wave drawn below the compressional wave is merely a device for simplifying the concept and relating it to the type of wave illustration commonly used in discussions of electromagnetic waves.
When an advancing wave encounters a medium of different character, some of its energy is reflected back into the initial medium, and some is transmitted into the second medium.
Reflection of Sound Waves
To understand wave reflection, it is helpful to think of the wave as a ray. A ray is a line which indicates the direction the wave is traveling. In a uniform medium, a ray will travel in a straight line. Only at the boundary of two media or in an area where the medium is changing do the rays change their direction.
If a line, called a "normal," is drawn perpendicular to a boundary, the angle between an incoming ray and this normal is called the angle of incidence, "i" as shown in figure 7-48. The angle which the reflected ray makes with the normal is called the angle of reflection "r." Any wave being reflected is reflected in such a way that the angle of incidence equals the angle of reflection.
Light is often thought of first when reflection is discussed; however, reflection is equally common in other types of waves. As an example, echoes are caused by reflection of sound waves.
When a hard surface is situated so that a sound reflection from it is outstanding, it appears as a distinct echo, and is heard an appreciable interval later than the direct sound. If the surface is concave, it may have a focusing effect and concentrate the reflected sound energy at one locality. Such a reflection may be several levels higher in intensity than the direct sound, and its arrival at a later time may have particular significance in such applications as sonar.
Speed of Sound
In any uniform medium, under given physical conditions, sound travels at a definite speed. In some substances, the velocity of sound is higher than in others. Even in the same medium under different conditions of temperature, pressure, etc., the velocity of sound varies. Density and elasticity of a medium are the two basic physical properties which govern the velocity of sound.
In general, a difference in density between two substances is sufficient to indicate which one will be the faster transmission medium for sound. For example, sound travels faster through water than it does through air at the same temperature. However, there are some surprising exceptions to this rule of thumb. An outstanding example among these exceptions involves comparison of the speed of sound in lead and aluminum at the same temperature. Sound travels at 16,700 fps in aluminum at 20° C, and only 4,030 fps in lead at 20° C, despite the fact that lead is much more dense than aluminum. The reason for such exceptions is found in the fact, mentioned above, that sound velocity depends on elasticity as well as density.
Using density as a rough indication of the speed of sound in a given substance, it can be stated as a general rule that sound travels fastest in solid materials, slower in liquids, and slowest in gases.
For a fixed temperature, the velocity of sound is constant for any medium and is independent of the period, frequency, or amplitude of the disturbance. Thus, the velocity of sound in air at 0° C (32° F) is 1,087 fps and increases by 2 fps for each centigrade degree of temperature rise (1.1 fps for each degree Fahrenheit). For practical purposes, the speed of sound in air may be considered 1,100 fps.
Mach Number
In the study of aircraft that fly at supersonic speeds, it is customary to discuss aircraft speed in relation to the velocity of sound (approximately 750 miles per hour). The term "Mach number" has been given to the ratio of the speed of an aircraft to the speed of sound, in honor of Ernst Mach, an Austrian scientist.
Thus, if the speed of sound at sea level is 750 miles per hour, an aircraft flying at a Mach number of 2.2 would be traveling at a speed of 750 mph x 2.2 = 1,650 miles per hour.
Frequency of Sound
The term "pitch" is used to describe the frequency of a sound. The outstanding recognizable difference between the tones produced by two different keys on a piano is a difference in pitch. The pitch of a tone is proportional to the number of compressions and rarefactions received per second, which in turn, is determined by the vibration frequency of the sounding source.
Frequency, or pitch, is usually measured by comparison with a standard. The standard tone may be produced by a tuning fork of known frequency or by a siren whose frequency is computed for a particular speed of rotation. By regulating the speed, the pitch of the siren is made equal to that of the tone being measured.
Loudness
When a bell rings, the sound waves spread out in all directions and the sound is heard in all directions. When a bell is struck lightly, the vibrations are of small amplitude and the sound is weak. A stronger blow produces vibrations of greater amplitude in the bell, and the sound is louder. It is evident that the amplitude of the air vibrations is greater when the amplitude of the vibrations of the source is increased. Hence, the loudness of the sound depends on the amplitude of the vibrations of the sound waves. As the distance from the source increases, the energy in each wave spreads out, and the sound becomes weaker.
The intensity of sound is the energy per unit area per second. In a sound wave of simple harmonic motion, the energy is half kinetic and half potential; half is due to the speed of the particles, and half is due to the compression and rarefaction of the medium. These two energies are 90 degrees out of phase at any instant. That is, when the speed of particle motion is at a maximum, the pressure is normal, and when the pressure is at a maximum or a minimum, the speed of the particles is zero.
The loudness of sound depends upon both intensity and frequency. The intensity of a sound wave in a given medium is proportional to the following quantities:
(1) Square of the frequency of vibration.
(2) Square of the amplitude.
(3) Density of the medium.
(4) Velocity of propagation.
At any distance from a source of sound (point), the intensity of the wave varies inversely as the square of the distance from the source.
As the sound wave advances, variations in pressure occur at all points in the transmitting medium. The greater the pressure variations, the more intense the sound wave will be. It can be shown that the intensity is proportional to the square of the pressure variation regardless of the frequency. Thus, by measuring pressure changes, the intensities of sounds having different frequencies can be compared directly.
Measurement of Sound Intensity
The loudness (intensity) of sound is not measured by the same type of scale used to measure length. The human ear has a nonlinear response pattern, and units of sound measurement are used that vary logarithmically with the amplitude of the sound variations. These units are the "bel" and "decibel," which refer to the difference between sounds of unequal intensity or sound levels. The decibel, which is one-tenth of a bel, is the minimum change of sound level perceptible to the human ear. Hence, the decibel merely describes the ratio of two sound levels. For example, 5 decibels may represent almost any volume of sound, depending on the intensity of the reference level or the sound level on which the ratio is based.