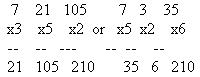
Addition of Whole Numbers
The process of finding the combined amount of two or more numbers is called addition. The answer is called the sum.
When adding several whole numbers, such as 4567, 832, 93122, and 65, place them under each other with their digits in columns so that the last, or right hand, digits are in the same column.
When adding decimals such as 45.67, 8.32, 9.8122, and 0.65, place them under each other so that the decimal points are in a straight "up-and-down" line.
To check addition, either add the figures again in the same order, or add them in reverse order.
Subtraction of Whole Numbers
Subtraction is the process of finding the difference between two numbers by taking the smaller from the larger of the two numbers. The number which is subtracted is called the subtrahend, the other number the minuend, and their difference is called the remainder. To find the remainder, write the subtrahend under the minuend, as in addition. Beginning at the right, subtract each figure in the subtrahend from the figure above it and write the individual remainder below in the same column. When the process is completed, the number below the subtrahend is the remainder.
To check subtraction, add the remainder and the subtrahend together. The sum of the two should equal the minuend.
Multiplication of Whole Numbers
The process of finding the quantity obtained by repeating a given number a specified number of times is called multiplication. More simply stated, the process of multiplication is, in effect, a case of repeated addition in which all the numbers being added are identical. Thus, the sum of 6 + 6 + 6 + 6 = 24 can be expressed by multiplication as 6 x 4 = 24. The numbers 6 and 4 are known as the factors of the multiplication, and 24 as the product.
In multiplication, the product is formed by multiplying the factors. When one of the factors is a single digit integer (whole number), the product is formed by multiplying the single digit integer with each digit of the other factor from right to left, carrying when necessary.
When both factors are multiple digit integers, the product is formed by multiplying each digit in the multiplying factor with the other factor. Exercise care, when writing down the partial products formed, to make certain that the extreme right digit lines up under the multiplying digit. It is then a matter of simple addition to find the final product.
EXAMPLE
Determine the cost of 18 spark plugs that cost $3.25 each.
3.25
x 18
----
2600
325
----
58.50
When multiplying a series of numbers together, the final product will be the same regardless of the order in which the numbers are arranged.
EXAMPLE
MULTIPLY: (7) (3) (5) (2) = 210
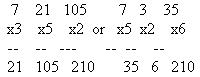
Division of Whole Numbers
The process of finding how many times one number is contained in a second number is called division. The first number is called the divisor, the second the dividend, and the result is the quotient.
Of the four basic operations with integers, division is the only one that involves trial and error in its solution. It is necessary to guess at the proper quotient digits, and though experience will tend to lessen the number of trials, everyone will guess incorrectly at some time or another.
Placing the decimal point correctly in the quotient quite often presents a problem. When dividing a decimal by a decimal, an important step is to first remove the decimal from the divisor. This is accomplished by shifting the decimal point to the right the number of places needed to eliminate it. Next, move the decimal point to the right as many places in the dividend as was necessary to move it in the divisor, and then proceed as in ordinary division.