Increasing the power by advancing the throttle produces a marked difference in the rate of climb. Climb depends upon the reserve power or thrust. Reserve power is the available power over and above that required to maintain horizontal flight at a given speed. Thus, if an airplane is equipped with an engine which produces 200 total available horsepower and the airplane requires only 130 horsepower at a certain level flight speed, the power available for climb is 70 horsepower.
Although we sometimes use the terms "power" and "thrust"
interchangeably, erroneously implying that they are synonymous, it is well
to distinguish between the two when discussing climb performance. Work
is the product of a force moving through a distance and is usually independent
of time. Work is measured by several standards, the most common unit is
called a "foot-pound." If a 1 pound mass is raised 1 foot, a work unit
of 1 foot-pound has been performed. The common unit of mechanical power
is horsepower; one horsepower is work equivalent to lifting 33,000 pounds
a vertical distance of 1 foot in 1 minute. The term "power," implies work
rate or units of work per unit of time, and as such is a function of the
speed at which the force is developed. "Thrust," also a function of work,
means the force which imparts a change in the velocity of a mass. This
force is measured in pounds but has no element of time or rate. It can
be said then, that during a steady climb, the rate of climb is a function
of excess thrust.

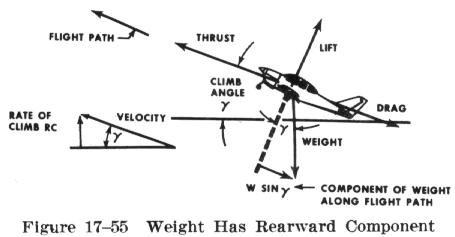
When the airplane is in steady level flight or with a slight
angle of climb, the vertical component of lift is very nearly the same
as the actual total lift. Such climbing flight would exist with the lift
very nearly equal to the weight. The net thrust of the powerplant may be
inclined relative to the flightpath but this effect will be neglected here
for the sake of simplicity. Although the weight of the airplane acts vertically,
a component of weight will act rearward along the flightpath (Fig. 17-55).
If it is assumed that the airplane is in a steady climb
with essentially a small inclination of the flightpath, the summation of
forces along the flightpath resolves to the following:
Forces forward = Forces aft
The basic relationship neglects some of the factors which may be of importance for airplanes of very high climb performance. (For example, a more detailed consideration would account for the inclination of thrust from the flightpath, lift not being equal to weight, a subsequent change of induced drag, etc.) However this basic relationship will define the principal factors affecting climb performance.
This relationship means that, for a given weight of the
airplane, the angle of climb depends on the difference between thrust and
drag, or the excess thrust (Fig. 17-56). Of course, when the excess thrust
is zero, the inclination of the flightpath is zero and the airplane will
be in steady, level flight. When the thrust is greater than the drag, the
excess thrust will allow a climb angle depending on the value of excess
thrust. On the other hand, when the thrust is less than the drag, the deficiency
of thrust will allow an angle of descent.
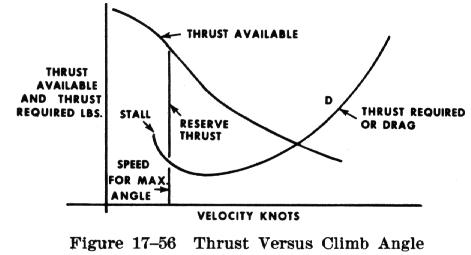
The most immediate interest in the climb angle performance involves obstacle clearance. The most obvious purpose for which it might be used is to clear obstacles when climbing out of short or confined airports.
The maximum angle of climb would occur where there exists the greatest difference between thrust available and thrust required; i.e., for the propeller powered airplane, the maximum excess thrust and angle of climb will occur at some speed just above the stall speed. Thus, if it is necessary to clear an obstacle after takeoff, the propeller powered airplane will attain maximum angle of climb at an airspeed close to - if not at - the takeoff speed.
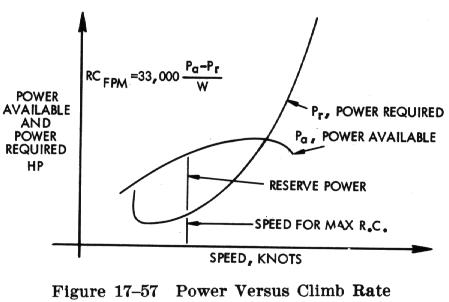
Of greater general interest in climb performance are the factors which affect the rate of climb. The vertical velocity of an airplane depends on the flight speed and the inclination of the flightpath. In fact, the rate of climb is the vertical component of the flightpath velocity.
For rate of climb, the maximum rate would occur where there
exists the greatest difference between power available and power required
(Fig. 17-57). The above relationship means that, for a given weight of
the airplane, the rate of climb depends on the difference between the power
available and the power required, or the excess power. Of course, when
the excess power is zero, the rate of climb is zero and the airplane is
in steady level flight. When power available is greater than the power
required, the excess power will allow a rate of climb specific to the magnitude
of excess power.
It can be said, then, that during a steady climb, the rate of climb will depend on excess power while the angle of climb is a function of excess thrust.
The climb performance of an airplane is affected by certain variables. The conditions of the airplane's maximum climb angle or maximum climb rate occur at specific speeds, and variations in speed will produce variations in climb performance. Generally, there is sufficient latitude in most general aviation airplanes that small variations in speed from the optimum do not produce large changes in climb performance, and certain operational considerations may require speeds slightly different from the optimum. Of course, climb performance would be most critical with high gross weight, at high altitude, in obstructed takeoff areas, or during malfunction of a powerplant. Then, optimum climb speeds are necessary.
Weight has a very pronounced effect on airplane performance. If weight is added to the airplane, it must fly at a higher angle of attack to maintain a given altitude and speed. This increases the induced drag of the wings, as well as the parasite drag of the airplane. Increased drag means that additional power is needed to overcome it, which in turn means that less reserve power is available for climbing. Airplane designers go to great effort to minimize the weight since it has such a marked effect on the factors pertaining to performance.
A change in the airplane's weight produces a twofold effect on climb performance. First, the weight affects both the climb angle and the climb rate. In addition, a change in weight will change the drag and the power required. This alters the reserve power available. Generally, an increase in weight will reduce the maximum rate of climb but the airplane must be operated at some increase of climb speed to achieve the smaller peak climb rate.
An increase in altitude also will increase the power required and decrease the power available. Hence, the climb performance of an airplane is affected greatly by altitude. The speeds for maximum rate of climb, maximum angle of climb, and maximum and minimum level flight airspeeds vary with altitude. As altitude is increased, these various speeds finally converge at the absolute ceiling of the airplane. At the absolute ceiling, there is no excess of power and only one speed will allow steady level flight. Consequently, the absolute ceiling of the airplane produces zero rate of climb. The service ceiling is the altitude at which the airplane is unable to climb at a rate greater than 100 feet per minute. Usually, these specific performance reference points are provided for the airplane at a specific design configuration.
In discussing performance, it frequently is convenient
to use the terms "power loading" and "wing loading." Power loading is expressed
in pounds per horsepower and is obtained by dividing the total weight of
the airplane by the rated horsepower of the engine. It is a significant
factor in the airplane's takeoff and climb capabilities. Wing loading is
expressed in pounds per square foot and is obtained by dividing the total
weight of the airplane in pounds by the wing area (including ailerons)
in square feet. It is the airplane's wing loading that determines the landing
speed. These factors are discussed in subsequent sections of this chapter.